


: ファジィ推論法2
: ファジィ推論の概要
: ファジィ推論あるいはファジィ制御とは
目次
ここで紹介するファジィ推論法が最も簡単で基本的なものであるが,実用的な価値は高く,現に実用化されているファジィ制御システムのほとんどは,この推論方式に基づいているといってよい.これは後に述べるファジィ関係の合成則に基づくもので,Mandaniによって最初に応用された.
まず推論法1の一般型を考える前に,具体例を考えるのがわかりやすい.いまここで,風呂の湯の温度を快適な温度に保つために,ガス栓の開閉度を制御する問題を考える.この制御のためには,例えば,次のように2つの
if (前件部) then (後件部)
型の規則(あるいはルール)を表す命題を基に,制御量(ガス栓の開閉度)を推論すればよいだろう.ただし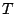 は「湯の温度」を表す変数,
は「湯の温度」を表す変数,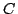 は「ガス栓の開き加減」を表す変数である.
は「ガス栓の開き加減」を表す変数である.
規則1: if
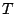
is 「かなり低い」 then
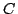
is 「やや強火」
規則2: if
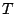
is 「かなり高い」 then
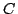
is 「やや弱火」
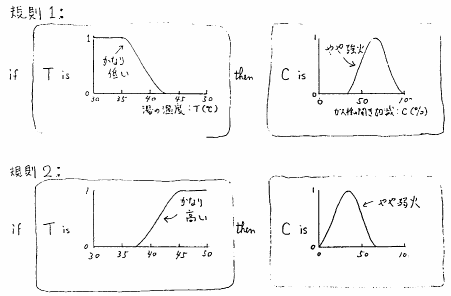
ここで,「かなり低い」,「かなり高い」,「やや強火」,「やや弱火」などの言語概念は,それぞれ,「湯の温度」や「ガス栓の開き加減」という全体集合中のファジィ集合として表される.これを図示すれば,例えば図3.1のようになろう.これらの規則は,「湯の温度がかなり低ければ,ガス栓の開き加減をやや強火のところにする.」,「湯の温度がかなり高ければ,ガス栓の開き加減をやや弱火のところにする.」という人間が普通に行う常識的な制御知識をそのまま表現したものである.
図 3.1
湯温調節のためのファジィ規則
 |
このようにすると,観測された事実から上のルールに則って制御変数値が推論することができ,さらに推論結果を用いて制御を行うことができる.例えばここで,観測事実として「湯の温度が少し高い」が,即ち,
事実:
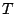
is 「少し高い」
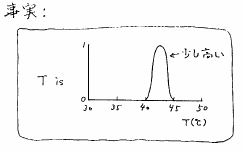
という命題が得られたとしよう.ここで,「少し高い」は図3.2のようにファジィ集合として表現できる.
図 3.2
湯温に関する観測事実
 |
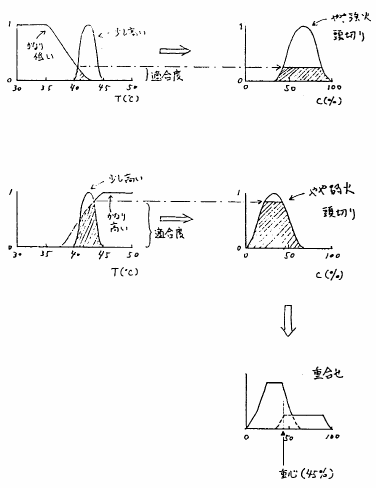
このとき推論は,図3.3のように行われる.つまり,
- 事実と各規則の前件部を照合して,各規則の適合度を算出する.
- 各規則の適合度に対応して,それぞれの規則の後件部を修正する.
- それぞれの規則の後件部を重ね合わせる.
- 重ね合わせた結果得られるファジィ集合の重心から制御量を求める.
図 3.3
湯温調節のためのファジィ推論過程
 |
1.の各規則の適合度は,それぞれの条件の前件部のファジィ集合と事実のファジィ集合との間の共通ファジィ集合をとったとき,その共通ファジィ集合の最高グレードとして得られる.つまり,共通ファジィ集合の一番高いところの高さである.この適合度は,各規則の前件部がどの程度観測事実と合っているかを0から1の間の値で示していると考えられる,つまり適合度は,その規則の前件部つまり仮定が現在の観測事実とどの程度合致していて,その規則がどの程度適用されるべきかという指標を与える.
2.では,適合度の値により結論部のファジィ集合の頭切りを行う.これは,規則の適合度によって後件部,つまりその規則の導く結論を制御していると見ることができる.
3.では,各条件の導く結論を重ね合わせてすべての規則の結論を結合した全体の結論を得ている.ここで結論もファジィ集合となっている.
4.結論のファジィ集合の重心の点を採ることにより,制御量を決定する.この例では,「制御量:ガス栓の開け加減」として「45%開ける」という結論が得られている.
ここで,4.は,制御量が3.の結果のようなファジィ集合で表されていては実際の栓の開閉制御が行えないため,制御量としてある代表点を一点選出する操作である.問題がもし制御でなくて人間の推論結果の提示が目的であれば,3.の段階のまま,つまりファジィ集合のままでグラフィカルに表現された方が人間としては,推論結果を的確に把握しやすい.
またもし湯の温度の観測が,温度センサなどによって機械的に行われるのであれば観測事実は,
事実:
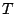
is 「42.5度」
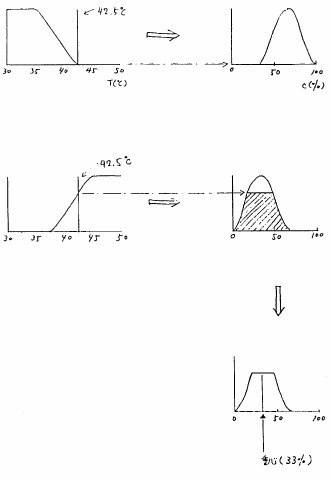
というようにクリスプに与えられるであろうが,この場合でも同様にして,図3.4のようにファジィ推論を行うことができる.
図 3.4
クリスプな観測事実に対するファジィ推論過程
|
|
上の推論を大ざっぱにいえば,ファジィ命題による規則を並列的にならべておき,各規則の後件部をその規則の適合度によって重み付けし,その平均をとったものを推論結果としていると見ることができる.
この例では,「湯の温度がかなり低い」ときと「湯の温度がかなり高い」ときの二つの場合にしか制御規則が与えられていないにも関わらず,「湯の温度が少し高い」場合の制御量の推論が的確に行われており,簡単な規則でかなりきめの細かい制御ができることをうかがわせる.
上の例では,規則の前件部の変数としてただひとつ「湯の温度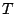 」しか用いなかった.しかし,一般には,変数の数は複数となり,規則は,次のように与えられるだろう.
」しか用いなかった.しかし,一般には,変数の数は複数となり,規則は,次のように与えられるだろう.
規則1: if {(
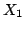
is
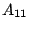
) and (
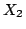
is
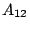
) and ...} then
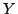
is
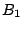
規則2: if {(
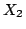
is
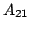
) and (
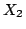
is
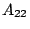
) and ...} then
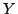
is
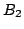
規則
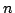
: if {(
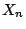
is
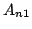
) and (
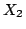
is
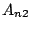
) and ...} then
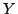
is
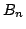
ここで,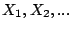 はそれぞれ前件部の変数であり,
はそれぞれ前件部の変数であり,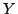 は後件部の変数(制御の場合は制御量)である.また
は後件部の変数(制御の場合は制御量)である.また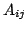 と
と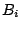 はファジィ集合で,
はファジィ集合で,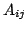 は規則
は規則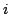 における変数
における変数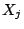 に対する条件を,
に対する条件を,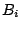 は規則
は規則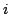 による
による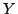 の推論結果を表してる.例えば,規則の数を
の推論結果を表してる.例えば,規則の数を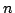 を2とし,変数も
を2とし,変数も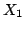 ひとつのみとし,
ひとつのみとし,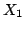 を
を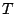 ,
,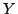 を
を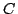 ,
,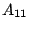 を「かなり低い」,
を「かなり低い」,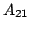 を「かなり高い」,
を「かなり高い」,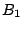 を「やや強火」,
を「やや強火」,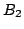 を「やや弱火」とおけば,上の温度調節の例題になる.
さて上の規則に対して観測事実は,複数の変数に対して
を「やや弱火」とおけば,上の温度調節の例題になる.
さて上の規則に対して観測事実は,複数の変数に対して
事実: (
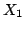
is
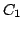
) and (
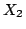
is
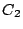
) ...
というかたちで与えられ,これより,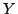 の値を推論することになる.ここで,一般型の推論方法は,先の湯温調節の例題と基本的には同じになる.ただし,各規則の前件部は複数の変数を含むため,前件部の適合度をどうやって求めるかが問題となる.結果的には非常に簡単で,それぞれの変数の適合度をすべて求めて,その規則内での最も小さい適合度をその規則の適合度とする.最も小さい適合度を採用するということは,前件部のそれぞれの変数に対する条件がandで結合されていることに由来する.
規則,変数の数とも2とし,
の値を推論することになる.ここで,一般型の推論方法は,先の湯温調節の例題と基本的には同じになる.ただし,各規則の前件部は複数の変数を含むため,前件部の適合度をどうやって求めるかが問題となる.結果的には非常に簡単で,それぞれの変数の適合度をすべて求めて,その規則内での最も小さい適合度をその規則の適合度とする.最も小さい適合度を採用するということは,前件部のそれぞれの変数に対する条件がandで結合されていることに由来する.
規則,変数の数とも2とし,
から
推論結果:
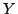
is
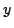
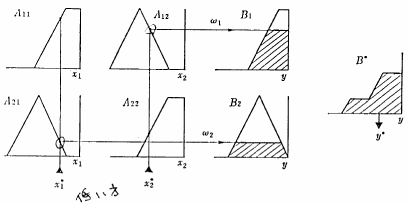
が得られる過程を図3.5に図示する.
図 3.5
推論法1 (a)
 |
推論法1にも適合度の算出と後件部の変形の仕方や,後件部の合成の仕方,さらに代表点の算出の仕方によってバリエーションがある.
図 3.6
推論法1 (b)
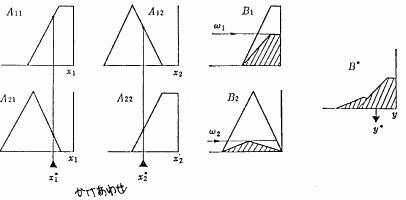 |
適合度については,ある規則内のそれぞれの変数に対する適合度のうちの最小のものをその規則の適合度とするのではなく,規則内のすべての変数の適合度の積をその規則の適合度とするほうほうがある.またこの場合,後件部のファジィ集合は適合度で頭切りされるのではなく,全体に適合度が乗算され結果的に押しつぶされた形となる(図3.6参照).これは,数学的には,ファジィ集合の交わりの定義の違いによるものであるが,詳しくは,5.6節で述べることにする.
後件部の合成の仕方としては,重ね合わせ法のほかに,それぞれの規則の後件部の修正後のファジィ集合を加算する方法も提案されている.ただし,この数学的な意味は,必ずしも明確であるとはいえないと思われる.
代表点の算出法(これは,非ファジィ化法とも呼ばれる)にも重心法の他に最大平均法,中央値法,乱数法などのいろいろな種類がある.可能性分布としてファジィ集合の形で与えられる推論結果からある一つの値を選択するのであるから本質的にいろいろな選択法が考えられる.ファジィ理論はあくまでも可能性分布を与えるのであり,この非ファジィ化法に対しては,ファジィ理論が数学的な根拠を与えるものではないと思われる.
この推論法の種々のバリエーションに対する評価は,文献[M-5]に詳しいので参照されたい.
上の文献では,ある特定の制御問題を種々のバリエーションで実行して,その制御結果の善し悪しで評価しているが,これが必ずしも一般に他の制御や推論問題に対してもいえることかどうかは吟味する必要がある.また推論方法の中には,ファジィ理論による数学的な裏付けの乏しいと思われるものも含まれていることも注意した方がよいだろう.ただ,ここでひとつ重要なことは,いろいろなバリエーションを用いてもそれほど決定的な違いは認められないことである.若干の差は認められるが本質的には,各方法ともにほぼ妥当に動作する.これは,ファジィ推論のアルゴリズムとしての丈夫さを示すもので,ファジィ理論が実用に具されうる由縁でもあろう.あまり敏感なアルゴリズムでは,実用には恐くて採用できない.



: ファジィ推論法2
: ファジィ推論の概要
: ファジィ推論あるいはファジィ制御とは
目次
平成12年5月17日
![]() はそれぞれ前件部の変数であり,
はそれぞれ前件部の変数であり,![]() は後件部の変数(制御の場合は制御量)である.また
は後件部の変数(制御の場合は制御量)である.また![]() と
と![]() はファジィ集合で,
はファジィ集合で,![]() は規則
は規則![]() における変数
における変数![]() に対する条件を,
に対する条件を,![]() は規則
は規則![]() による
による![]() の推論結果を表してる.例えば,規則の数を
の推論結果を表してる.例えば,規則の数を![]() を2とし,変数も
を2とし,変数も![]() ひとつのみとし,
ひとつのみとし,![]() を
を![]() ,
,![]() を
を![]() ,
,![]() を「かなり低い」,
を「かなり低い」,![]() を「かなり高い」,
を「かなり高い」,![]() を「やや強火」,
を「やや強火」,![]() を「やや弱火」とおけば,上の温度調節の例題になる.
さて上の規則に対して観測事実は,複数の変数に対して
を「やや弱火」とおけば,上の温度調節の例題になる.
さて上の規則に対して観測事実は,複数の変数に対して