


: 種々のファジィ集合演算子
: ファジィ理論の数学的基礎
: ファジィ集合とメンバシップ関数
目次
4.1節に述べたように,メンバシップ関数によってファジィ集合そのものは定義されるが,これだけでは数学にならない.ここにファジィ集合間の演算が定義されてはじめてファジィ理論が展開する.その基礎となるのが,2.4節でもふれた,包含,交わり(共通集合),結び(和集合),補集合である.本節では,これらの基本演算がどう定義されるかについて整理し,さらにそれらの演算に関して成り立つファジィ集合の性質を整理する.
ファジィ集合における4つの基本演算(包含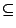 ,交わり
,交わり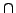 ,結び
,結び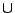 ,補集合not())は,通常,2.4節で述べたように定義されることが多い,しかし,一般には,ファジィ集合の基本演算の定義の基となる演算子には,種々のものが考えられ,どの演算子によってファジィ集合の基本演算を定義するかによって種々のファジィ理論が導かれる.事実,基本演算としては無駄に考えられるのであるが,どのような演算子を用いてもファジィ理論が展開できるわけではなく,そこには一定の枠組みがある.大ざっぱにいうと以下のようになる.まず4つの演算の中でもっとも基本的なものが包含(
,補集合not())は,通常,2.4節で述べたように定義されることが多い,しかし,一般には,ファジィ集合の基本演算の定義の基となる演算子には,種々のものが考えられ,どの演算子によってファジィ集合の基本演算を定義するかによって種々のファジィ理論が導かれる.事実,基本演算としては無駄に考えられるのであるが,どのような演算子を用いてもファジィ理論が展開できるわけではなく,そこには一定の枠組みがある.大ざっぱにいうと以下のようになる.まず4つの演算の中でもっとも基本的なものが包含(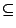 )である.この定義については,唯一(2.4節で定義されたもの)と考えていいだろう.つぎにある種の積演算子(後に説明する「
)である.この定義については,唯一(2.4節で定義されたもの)と考えていいだろう.つぎにある種の積演算子(後に説明する「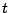 - ノルム」と呼ばれるものであればよい.)を用いて交わり(
- ノルム」と呼ばれるものであればよい.)を用いて交わり(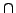 )が定義される.さらにある否定演算子(これも後に述べる)を用いて補集合(not())が定義される.最後の結び(
)が定義される.さらにある否定演算子(これも後に述べる)を用いて補集合(not())が定義される.最後の結び(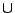 )はある種の和演算子(後に述べる「
)はある種の和演算子(後に述べる「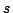 - ノルム」と呼ばれるもの)によって定義されるのだが,ここでこの和演算子は,先に選んだ積演算子と否定演算子によって唯一に決まってしまう.和演算子としては先に選んだ積演算子(選んだ否定演算の意味で)
- ノルム」と呼ばれるもの)によって定義されるのだが,ここでこの和演算子は,先に選んだ積演算子と否定演算子によって唯一に決まってしまう.和演算子としては先に選んだ積演算子(選んだ否定演算の意味で)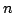 - 双対(次節で説明する)な和演算子を選ばなくてはならないのである.このようにファジィ集合の基本演算を選ぶ限りにおいては,表4.1のようなファジィ集合の基本性質が成立する(但し表4.1では,補集合not(
- 双対(次節で説明する)な和演算子を選ばなくてはならないのである.このようにファジィ集合の基本演算を選ぶ限りにおいては,表4.1のようなファジィ集合の基本性質が成立する(但し表4.1では,補集合not( )を
)を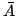 と表記している).つまり,包含を定義のとおりとし,任意の
と表記している).つまり,包含を定義のとおりとし,任意の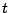 - ノルムと,任意の否定演算子を選び,それらに基づいて3つの基本演算(交わり,結び,否定)を定義する限りにおいては,どの基本演算を採用しようと,表4.1のファジィ集合の基本性質が成立し,ファジィ理論を展開することができる.しかもこの限りにおいては,クリスプ集合に対して,いずれのファジィ集合基本演算を適用しようとも,すべて結果は,通常の集合演算の結果と一致し,通常の集合論の拡張となる.ファジィ集合の基本性質は,表4.1のように通常の集合の基本性質をほとんど満足するが,(12)のように,クリスプ集合で成立する相補律(排中律と矛盾律)だけはファジィ集合において成立しない.したがってファジィ集合は,クリスプ集合のように「ブール束」は成しておらず,それよりすこしゆるい「分配束」を成しているといえる.
- ノルムと,任意の否定演算子を選び,それらに基づいて3つの基本演算(交わり,結び,否定)を定義する限りにおいては,どの基本演算を採用しようと,表4.1のファジィ集合の基本性質が成立し,ファジィ理論を展開することができる.しかもこの限りにおいては,クリスプ集合に対して,いずれのファジィ集合基本演算を適用しようとも,すべて結果は,通常の集合演算の結果と一致し,通常の集合論の拡張となる.ファジィ集合の基本性質は,表4.1のように通常の集合の基本性質をほとんど満足するが,(12)のように,クリスプ集合で成立する相補律(排中律と矛盾律)だけはファジィ集合において成立しない.したがってファジィ集合は,クリスプ集合のように「ブール束」は成しておらず,それよりすこしゆるい「分配束」を成しているといえる.
表 4.1
ファジィ集合の基本性質(
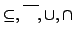 の場合)
の場合)
 |
4つの基本演算のうち,最も基本となるのは包含である.これは,2.4節で述べたように,すべての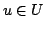 に対して,
に対して,
のとき,
と定義される.また,二つのメンバシップ関数がすべての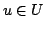 に対して一致する場合,即ち,
に対して一致する場合,即ち,
である場合,
という.
交わり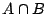 のメンバシップ関数は,一般に,ある積演算子(
のメンバシップ関数は,一般に,ある積演算子(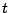 - ノルム)
- ノルム)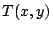 を用いて,すべての
を用いて,すべての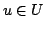 に対して,
に対して,
と定義される.ここで,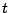 - ノルム
- ノルム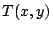 は,
は,
![$x(\in [0,1]),y(\in [0,1])$](img143.gif) に対して,区間
に対して,区間![$[0,1]$](img106.gif) の中のある値を返す関数であり,詳しくは次節に述べるようなものである.感覚的にいうと,
の中のある値を返す関数であり,詳しくは次節に述べるようなものである.感覚的にいうと,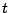 - ノルムは
- ノルムは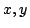 が互いに「制限しあうような」あるいは「足を引っ張りあうような」関数で,関数の値は,大きくとも
が互いに「制限しあうような」あるいは「足を引っ張りあうような」関数で,関数の値は,大きくとも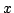 と
と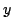 のうち小さい方と同じかそれより小さくなる.
のうち小さい方と同じかそれより小さくなる.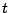 - ノルムとして,もっとも一般的に用いられる,
- ノルムとして,もっとも一般的に用いられる,
を採用した場合,この場合に限り,交わりの定義の特別な場合として,2.4節で示した交わりが定義される.
あるファジィ集合 の補集合not(
の補集合not( )のメンバシップ関数は,一般に,ある否定演算子
)のメンバシップ関数は,一般に,ある否定演算子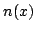 を用いて,すべての
を用いて,すべての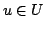 に対して,
に対して,
と表される.否定演算子は,詳しくは,4.3節に述べるとおりだが,簡単にいうと,![$x(\in [0,1])$](img148.gif) に対して区間
に対して区間![$[0,1]$](img106.gif) の中のある値を返す関数で,0に近い入力に対しては1に近い出力を出し,逆に1に近い入力に対しては0に近い出力を出す関数である.否定として,もっとも一般的に用いられるのが,
の中のある値を返す関数で,0に近い入力に対しては1に近い出力を出し,逆に1に近い入力に対しては0に近い出力を出す関数である.否定として,もっとも一般的に用いられるのが,
であり,この場合に限り,補集合の特別な場合として,2.4節で示した補集合が定義される.
結び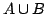 のメンバシップ関数は,一般に,ある和演算子(
のメンバシップ関数は,一般に,ある和演算子(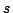 - ノルム)
- ノルム)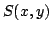 を用いて,すべての
を用いて,すべての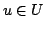 に対して,
に対して,
と定義される.ここで,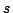 - ノルム
- ノルム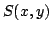 は,
は,
![$x(\in [0,1]),y(\in [0,1])$](img143.gif) に対して,区間
に対して,区間![$[0,1]$](img106.gif) の中のある値を返す関数であり,詳しくは次節に述べるとおりである.感覚的にいうと,
の中のある値を返す関数であり,詳しくは次節に述べるとおりである.感覚的にいうと,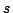 - ノルムは
- ノルムは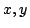 が互いに「助け合うような」関数で,関数の値は,少なくとも
が互いに「助け合うような」関数で,関数の値は,少なくとも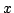 と
と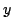 のうち大きい方と同じかそれより大きくなる.ここで,
のうち大きい方と同じかそれより大きくなる.ここで,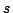 - ノルムとしては,無駄のものが考えられるが,
- ノルムとしては,無駄のものが考えられるが,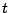 - ノルム
- ノルム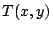 と否定
と否定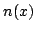 が決まればこれに対して「
が決まればこれに対して「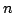 - 双対」な
- 双対」な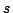 - ノルムはただ一つ決まる.もっとも一般的な場合,つまり,
- ノルムはただ一つ決まる.もっとも一般的な場合,つまり,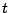 - ノルムを
- ノルムを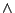 を用いて定義し,否定を
を用いて定義し,否定を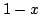 とした場合は,双対(否定の特別な場合,つまり,
とした場合は,双対(否定の特別な場合,つまり,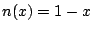 に基づく「
に基づく「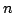 - 双対」は簡単に「双対」と呼ばれる.)な
- 双対」は簡単に「双対」と呼ばれる.)な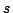 - ノルムは,
- ノルムは,
となり,この場合に限り,結びの特別な場合として,2.4節で示した結びが定義される.ここで,注意すべきは,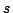 - ノルムとしては,交わりの定義に用いた
- ノルムとしては,交わりの定義に用いた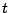 - ノルムと
- ノルムと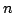 - 双対の関係にあるものを採用しなければ,ファジィ集合に関する基本的性質(図4.1)が成立しなくなり,ファジィ理論を展開できなくなることである.
実際には,否定としては,
- 双対の関係にあるものを採用しなければ,ファジィ集合に関する基本的性質(図4.1)が成立しなくなり,ファジィ理論を展開できなくなることである.
実際には,否定としては,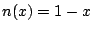 がほとんどの場合に用いられる.また交わりとしては,
がほとんどの場合に用いられる.また交わりとしては,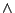 に基づいたもの(論理積)が多く,次節に述べる代数積や限界積に基づくものもときどき使われる.また結びとしては,論理積と双対の関係にある
に基づいたもの(論理積)が多く,次節に述べる代数積や限界積に基づくものもときどき使われる.また結びとしては,論理積と双対の関係にある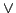 に基づいたもの(論理和)が多く用いられ,ついで,代数積,限界積とそれぞれ双対の関係にある,代数和,限界和に基づくものもときどき使われる.
上に述べたように,交わりと結びの定義は,互いに
に基づいたもの(論理和)が多く用いられ,ついで,代数積,限界積とそれぞれ双対の関係にある,代数和,限界和に基づくものもときどき使われる.
上に述べたように,交わりと結びの定義は,互いに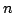 - 双対な関係にある
- 双対な関係にある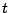 - ノルムと
- ノルムと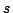 - ノルムを用いて行うべきで,互いに
- ノルムを用いて行うべきで,互いに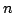 - 双対でない定義を混用するのは避けるべきであろう.しかし,文献によっては,ときどき混用されていると思われる場合も見受けられるので注意を要する.また後でその都度述べるが,演算子
- 双対でない定義を混用するのは避けるべきであろう.しかし,文献によっては,ときどき混用されていると思われる場合も見受けられるので注意を要する.また後でその都度述べるが,演算子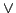 については,本節で述べた結びの定義に由来するものの他に,上限をとる操作に由来するものがあるので,これらの区別を明確にする必要がある.例えば,交わりを代数積に基づいて定義しているときに,結びの定義に由来する
については,本節で述べた結びの定義に由来するものの他に,上限をとる操作に由来するものがあるので,これらの区別を明確にする必要がある.例えば,交わりを代数積に基づいて定義しているときに,結びの定義に由来する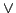 を用いると不都合なことが起こると予想されるが,上限をとる操作に由来する
を用いると不都合なことが起こると予想されるが,上限をとる操作に由来する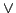 については,交わりの代数積と併用しても理論的に問題はない.
については,交わりの代数積と併用しても理論的に問題はない.
平成12年5月17日
