
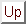


: 含意命題のファジィ関係による標準形表現
: ファジィ推論の数学的解釈
: ファジィ推論の数学的解釈
目次
通常,推論とは,複数の命題とその真偽が与えられて,それらの関係からある別の命題とその真偽を導くことである.このとき,あるひとつの命題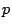 は一般に
は一般に
という形の標準形で表される.ここで, は変数の組を表し,変数の数が
は変数の組を表し,変数の数が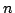 個の場合は,
個の場合は,
と表現される.また は,全体集合
は,全体集合
の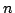 次元部分集合である.但し
次元部分集合である.但し
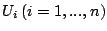 はそれぞれ変数
はそれぞれ変数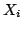 に対応する全体集合,即ち,値域である.
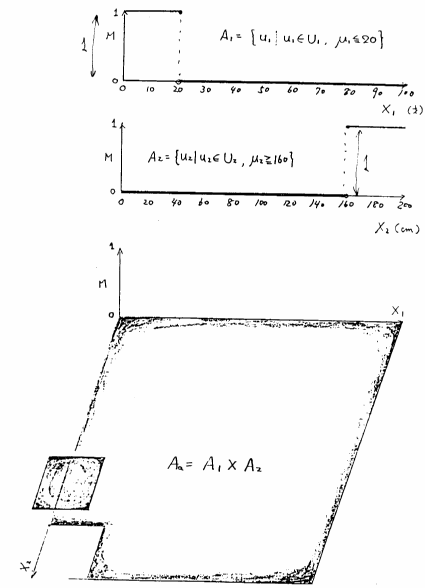
具体的な例を示すと,
に対応する全体集合,即ち,値域である.
具体的な例を示すと,
という命題の場合は,
とし,これらの定義域を
と便宜上,設定すれば(定義域は適当に変えてもよい),
なる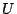 の2次元部分集合
の2次元部分集合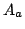 を用いて(図5.1参照),
を用いて(図5.1参照),
と標準形で表される.
図 5.1
2次元クリスプ集合:
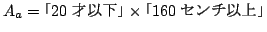
|
|
この標準形の第一の見方として,次のようなものがある.即ち,
「命題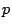 とは,その真偽が,変数の組
とは,その真偽が,変数の組 の値
の値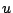 によって変化するもので,
によって変化するもので,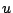 が集合
が集合 の要素ならば真であり,要素でなければ偽となる命題である.」
の要素ならば真であり,要素でなければ偽となる命題である.」
である.上の例では,
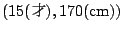 は
は の要素であるから,命題
の要素であるから,命題 は真であると主張され,また
は真であると主張され,また
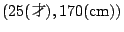 は
は の要素ではないから偽であると主張されるのだが,実際に,「太郎が15才で,背が170センチ」なら
の要素ではないから偽であると主張されるのだが,実際に,「太郎が15才で,背が170センチ」なら (「太郎は20才以下で,背が160センチ以上である.」)が真で,「太郎が25才で,背が170センチ」なら
(「太郎は20才以下で,背が160センチ以上である.」)が真で,「太郎が25才で,背が170センチ」なら は偽であることがわかる.
この標準形の第二の見方として,
は偽であることがわかる.
この標準形の第二の見方として,
「命題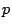 が真であると主張した場合,変数の組
が真であると主張した場合,変数の組 の値は,集合
の値は,集合 の要素になる可能性はあるが,要素以外になる可能性はない.」
の要素になる可能性はあるが,要素以外になる可能性はない.」
とみることができる.さらにいえば,
「命題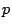 が真であると主張した場合,集合
が真であると主張した場合,集合 の特性関数
の特性関数 の値の可能性分布を表している.」
の値の可能性分布を表している.」
といっても同じである.上の例では,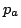 :「太郎が20才以下で,背が160センチ以上である.」が主張されたとき,これは,
:「太郎が20才以下で,背が160センチ以上である.」が主張されたとき,これは,
「 (
(
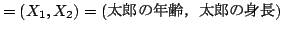 )の値のとりうる可能性としては
)の値のとりうる可能性としては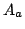 の要素すべてが候補として考えられ,
の要素すべてが候補として考えられ,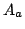 の要素以外となる可能性がまったくない」
の要素以外となる可能性がまったくない」
と,変数の組 のとりうる値の可能性にある制御が与えられることを意味するのだが,これが妥当であることは自明であろう.
このように通常の命題の標準形に現われる場合
のとりうる値の可能性にある制御が与えられることを意味するのだが,これが妥当であることは自明であろう.
このように通常の命題の標準形に現われる場合 は,「変数の組
は,「変数の組 のとりうるすべての値を,命題を真にするものと,偽にするものに二分するもの」とみることもできるし,「命題
のとりうるすべての値を,命題を真にするものと,偽にするものに二分するもの」とみることもできるし,「命題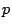 が真であるとき,変数の組
が真であるとき,変数の組 の値のとりうる可能性を制限するもの」とみなすこともできる.ここでは通常の命題について議論したのだが,この場合,集合
の値のとりうる可能性を制限するもの」とみなすこともできる.ここでは通常の命題について議論したのだが,この場合,集合 はクリスプな集合であることに注意されたい.これは,通常の意味での「命題」の概念では,その真偽が「真」か「偽」のどちらかにはっきりするもの以外「命題」と定義されないためであり,この結果,可能性も「ある」か「ない」かの二者択一となる.
上で考察した,通常の命題は,真偽のはっきりしている問題しか取り扱えなかった.そこで,この命題の定義を拡張して,真偽のあいまいな問題を取り扱えるようにしたのが「ファジィ命題」である.このファジィ命題においては,命題の真偽は,真(1),偽(0)の二者択一でなくてもよく,真理値として
はクリスプな集合であることに注意されたい.これは,通常の意味での「命題」の概念では,その真偽が「真」か「偽」のどちらかにはっきりするもの以外「命題」と定義されないためであり,この結果,可能性も「ある」か「ない」かの二者択一となる.
上で考察した,通常の命題は,真偽のはっきりしている問題しか取り扱えなかった.そこで,この命題の定義を拡張して,真偽のあいまいな問題を取り扱えるようにしたのが「ファジィ命題」である.このファジィ命題においては,命題の真偽は,真(1),偽(0)の二者択一でなくてもよく,真理値として![$[0,1]$](img106.gif) の中の任意の実数をとることができる.つまり,命題の真理値として,多値論理の拡張である,無限値論理を許すことに他ならない.このような拡張は,上で述べた通常の命題の標準形におけるクリスプ集合
の中の任意の実数をとることができる.つまり,命題の真理値として,多値論理の拡張である,無限値論理を許すことに他ならない.このような拡張は,上で述べた通常の命題の標準形におけるクリスプ集合 をファジィ集合(2次元以上のクリスプ集合のファジィ的拡張はファジィ関係と呼ばれるから,ファジィ関係といった方がより一般的)に拡張することにより,直ちに得られる.したがって,ファジィ命題の標準形も
をファジィ集合(2次元以上のクリスプ集合のファジィ的拡張はファジィ関係と呼ばれるから,ファジィ関係といった方がより一般的)に拡張することにより,直ちに得られる.したがって,ファジィ命題の標準形も
となり,ここで, が
が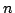 項ファジィ関係であることにさえ注意すればよい.
このファジィ命題の標準形を,通常の命題の第一の見方に対応させて考えると,これは,
項ファジィ関係であることにさえ注意すればよい.
このファジィ命題の標準形を,通常の命題の第一の見方に対応させて考えると,これは,
「ファジィ命題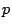 とは,その真理値が,変数の値
とは,その真理値が,変数の値 の値
の値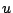 によって変化し,ファジィ関係
によって変化し,ファジィ関係 におけるグレード
におけるグレード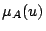 として与えられる命題である.」
として与えられる命題である.」
ということを意味していると考えることができる.
また第二の見方をすれば,
「ファジィ命題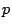 が真であると主張したとき,ファジィ関係
が真であると主張したとき,ファジィ関係 のメンバシップ関数が変数の組
のメンバシップ関数が変数の組 の値
の値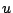 のとりうる可能性に制限を与える.」
のとりうる可能性に制限を与える.」
もう少し,具体的にいえば,
「ファジィ命題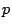 が真であると主張した場合,ファジィ関係
が真であると主張した場合,ファジィ関係 のメンバシップ関数が,
のメンバシップ関数が, の値の可能性分布を表している」
の値の可能性分布を表している」
ともいえる.
このようにファジィ命題の標準形に現われるファジィ関係 は,「変数の組
は,「変数の組 のとりうるすべての値に対して,命題
のとりうるすべての値に対して,命題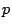 の真理値を与えるもの」とみることもできるし,「ファジィ命題
の真理値を与えるもの」とみることもできるし,「ファジィ命題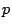 が真であるとき,変数の組
が真であるとき,変数の組 の値のとりうる可能性を制限するもの」とみなすことができる.
何れの見方にせよ,ファジィ命題においては,真理値あるいは可能性がファジィ関係のメンバシップ関数のグレードとして
の値のとりうる可能性を制限するもの」とみなすことができる.
何れの見方にせよ,ファジィ命題においては,真理値あるいは可能性がファジィ関係のメンバシップ関数のグレードとして![$[0,1]$](img106.gif) の中の任意の実数をとることができるため,例えば,
の中の任意の実数をとることができるため,例えば,
というような,真偽のはっきりしない(したがって,通常の命題ではない)主張をファジィ命題として取り扱うことができる.即ち,ファジィ命題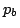 は,前項の通常の命題
は,前項の通常の命題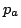 における集合
における集合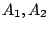 の代わりに,例えば図5.2の示すようなファジィ集合Young,Tallを用い,標準形の2次元集合
の代わりに,例えば図5.2の示すようなファジィ集合Young,Tallを用い,標準形の2次元集合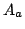 の代わりに,ファジィ関係
の代わりに,ファジィ関係
を用いれば,
と標準形で表される.
図
2項ファジィ関係:
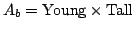
 |



: 含意命題のファジィ関係による標準形表現
: ファジィ推論の数学的解釈
: ファジィ推論の数学的解釈
目次
平成12年5月17日

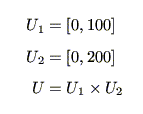
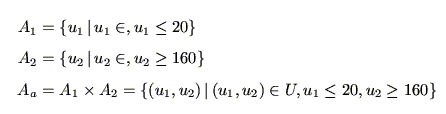
とは,その真偽が,変数の組
の値
によって変化するもので,
が集合
の要素ならば真であり,要素でなければ偽となる命題である.」
が真であると主張した場合,変数の組
の値は,集合
の要素になる可能性はあるが,要素以外になる可能性はない.」
が真であると主張した場合,集合
の特性関数
の値の可能性分布を表している.」
(
)の値のとりうる可能性としては
の要素すべてが候補として考えられ,
の要素以外となる可能性がまったくない」
とは,その真理値が,変数の値
の値
によって変化し,ファジィ関係
におけるグレード
として与えられる命題である.」
が真であると主張したとき,ファジィ関係
のメンバシップ関数が変数の組
の値
のとりうる可能性に制限を与える.」
が真であると主張した場合,ファジィ関係
のメンバシップ関数が,
の値の可能性分布を表している」