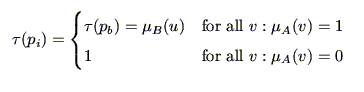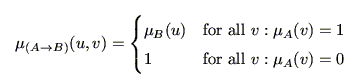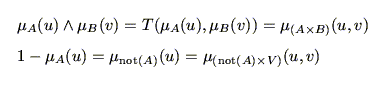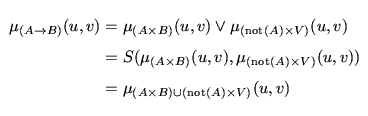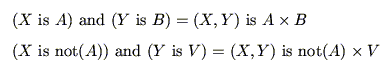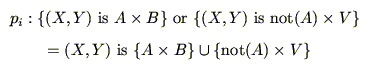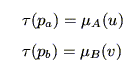


: ファジィ推論
: ファジィ推論の数学的解釈
: ファジィ命題とその標準形
目次
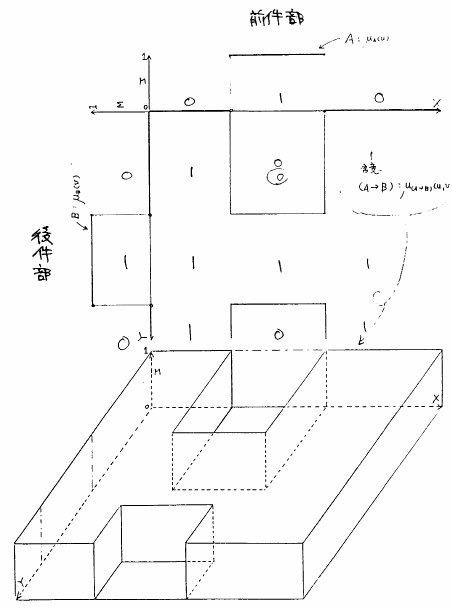
推論を行うときに非常に重要な役割を果たす命題として,含意命題と呼ばれるものがある.一般に,含意命題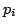 は,
は,
あるいは,もっと簡単には,
という形で表される命題で,推論における規則(ルール)は正にこの形の命題である.ここで,(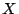 is
is  )は前件部,(
)は前件部,(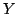 is
is 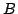 )は後件部と呼ばれ,それぞれが,それ自身で,5.1節で述べた命題となっている.したがって,この前件部の命題を
)は後件部と呼ばれ,それぞれが,それ自身で,5.1節で述べた命題となっている.したがって,この前件部の命題を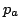 ,後件部の命題を
,後件部の命題を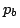 とすれば,
とすれば,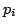 はさらに,
はさらに,
とも表現できる.なおここで, がファジィ関係ならば,
がファジィ関係ならば,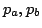 はファジィ命題となり,
はファジィ命題となり,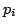 自体も通常の含意命題の拡張としての,ファジィ含意命題となる.
ところで,上の含意命題
自体も通常の含意命題の拡張としての,ファジィ含意命題となる.
ところで,上の含意命題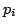 全体は,5.1節で述べた標準形をしておらず,このままでは,後に説明する推論を行う際に,取り扱いが面倒になる.そこで,本節では,このファジィ含意命題を標準形で記述する方法について述べる.アイディアとしては,まず,この含意命題全体の真理値を左右する変数の組を抽出する.つぎに変数の組の値によってこの含意命題の真理値がどのように変化するかを考察する.最後に,この真理値の変化に対応するファジィ関係を求める.こうすれば,この含意命題は,抽出した変数の組と求められたファジィ関係を用いて,標準形として表現できるはずである.
もう少し具体的に見ると次のようになる.含意命題
全体は,5.1節で述べた標準形をしておらず,このままでは,後に説明する推論を行う際に,取り扱いが面倒になる.そこで,本節では,このファジィ含意命題を標準形で記述する方法について述べる.アイディアとしては,まず,この含意命題全体の真理値を左右する変数の組を抽出する.つぎに変数の組の値によってこの含意命題の真理値がどのように変化するかを考察する.最後に,この真理値の変化に対応するファジィ関係を求める.こうすれば,この含意命題は,抽出した変数の組と求められたファジィ関係を用いて,標準形として表現できるはずである.
もう少し具体的に見ると次のようになる.含意命題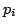 には,
には,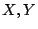 の2つの変数の組が含まれ,それらの値のとり方によって
の2つの変数の組が含まれ,それらの値のとり方によって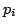 の真理値が支配されている.ここで,これらの変数の組を合併させた,
の真理値が支配されている.ここで,これらの変数の組を合併させた,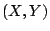 を1つの変数の組として考えれば,含意命題
を1つの変数の組として考えれば,含意命題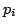 の真理値は,1つの変数の組
の真理値は,1つの変数の組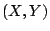 の値によってその真理値が支配されるとみなすことができる.ここで,
の値によってその真理値が支配されるとみなすことができる.ここで,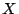 の定義域(即ち,
の定義域(即ち,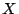 がとりうる値
がとりうる値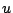 の全体集合)を
の全体集合)を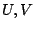 の定義域(即ち,
の定義域(即ち,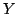 がとりうる値
がとりうる値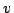 の全体集合)を
の全体集合)を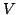 とすれば,変数の組
とすれば,変数の組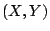 の定義域(即ち,
の定義域(即ち,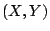 がとりうる値
がとりうる値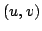 の全体集合)は
の全体集合)は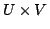 となる.したがって,
となる.したがって,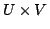 上に,あるファジィ関係
上に,あるファジィ関係
 を考え,このグレード
を考え,このグレード
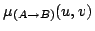 がすべての
がすべての
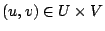 において,含意命題
において,含意命題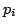 の真理値に一致するように
の真理値に一致するように
 のメンバシップ関数を定めれば,
のメンバシップ関数を定めれば,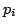 はこのファジィ関係
はこのファジィ関係
 を用いて,
を用いて,
と標準形で表現される.
次項以下では,ファジィ含意命題の真理値の変化について考察し,ファジィ命題の標準形を与えるファジィ関係
 のメンバシップ関数の具体的な形がいかに与えられるかについて説明する.
本報告書では,ファジィ含意命題の標準形を与えるファジィ関係の名前として,その意味が自明となるように
のメンバシップ関数の具体的な形がいかに与えられるかについて説明する.
本報告書では,ファジィ含意命題の標準形を与えるファジィ関係の名前として,その意味が自明となるように
 などを便宜上使うので,注意されたい.つまり
などを便宜上使うので,注意されたい.つまり
 などは単にある1つのファジィ関係を表しているにすぎない.
一般的にファジィ含意命題について議論する前に,通常の含意命題の場合は,どのように標準形表現されるかについて考察する.
通常の含意命題の場合は,含意命題
などは単にある1つのファジィ関係を表しているにすぎない.
一般的にファジィ含意命題について議論する前に,通常の含意命題の場合は,どのように標準形表現されるかについて考察する.
通常の含意命題の場合は,含意命題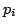 の真理値(真(1)か偽(0)のどちらか)は,前件部(命題)
の真理値(真(1)か偽(0)のどちらか)は,前件部(命題)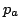 の真偽と後件部(命題)
の真偽と後件部(命題)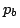 の真偽の組合せによって
の真偽の組合せによって
と与えられることは周知の事実である.これをみると,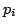 の真理値は,
の真理値は,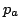 が真のときは
が真のときは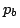 の真理値に従い,
の真理値に従い,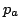 が偽のときは常に真となっている.ここで,「
が偽のときは常に真となっている.ここで,「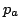 が真のとき」というのは「
が真のとき」というのは「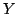 の値
の値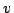 が
が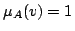 を満たすとき」であり「
を満たすとき」であり「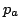 が偽のとき」というのは,「
が偽のとき」というのは,「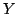 の値
の値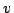 が
が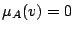 を満たすとき」であることに注意し,さらに
を満たすとき」であることに注意し,さらに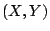 の値が
の値が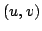 であるときの
であるときの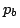 の真理値
の真理値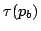 は
は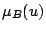 となることに注意すれば,
となることに注意すれば,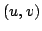 に対する
に対する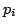 の真理値
の真理値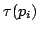 は,
は,
と得られることがわかる.したがってこの真理値の変化と一致するグレードの変化をもつメンバシップ関数
によって特徴付けられる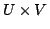 上のファジィ関係
上のファジィ関係
 を用いれば,通常の含意命題は,標準形表現される.(注意:ここでは,通常の含意について議論しているので,
を用いれば,通常の含意命題は,標準形表現される.(注意:ここでは,通常の含意について議論しているので,
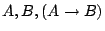 はすべてクリスプ集合であり,したがって,それらのグレードは
はすべてクリスプ集合であり,したがって,それらのグレードは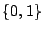 の何れかしかとらないことに注意.)
の何れかしかとらないことに注意.)
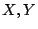 が共に1次元の変数である場合は,
が共に1次元の変数である場合は,
 は2次元集合となり,例えば図5.3のように図示することができる.
は2次元集合となり,例えば図5.3のように図示することができる.
図 5.3
通常のクリスプな含意命題の

 |
含意命題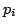 の
の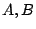 を一般にファジィ関係とした場合に,
を一般にファジィ関係とした場合に,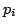 はファジィ含意命題となるのだが,この場合の標準形はどうなるだろうか.これの一つの答えが,ファジィ理論の提唱者Zadeh自身により提案されている.
Zadehの含意によれば,
はファジィ含意命題となるのだが,この場合の標準形はどうなるだろうか.これの一つの答えが,ファジィ理論の提唱者Zadeh自身により提案されている.
Zadehの含意によれば,
なるメンバシップ関数を持つファジィ関係
 が
が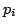 の標準形表現を与える.以下では,この意味を解釈する.
いま,
の標準形表現を与える.以下では,この意味を解釈する.
いま,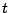 - ノルム,
- ノルム,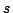 - ノルムとして,それぞれ論理積,論理和で採用する場合を考えると(この場合必然的に否定演算子
- ノルムとして,それぞれ論理積,論理和で採用する場合を考えると(この場合必然的に否定演算子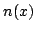 は
は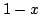 となることに注意)4.5節で述べた直積,円柱集合の定義から,
となることに注意)4.5節で述べた直積,円柱集合の定義から,
であることに注意すれば,
と置き換えられる.つまり,ファジィ関係
 は,実は,
は,実は,
である(むしろ,Zadehのファジィ含意の定義はこの形の方が本質的であり,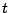 - ノルム,
- ノルム,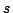 - ノルムの選び方で,
- ノルムの選び方で,
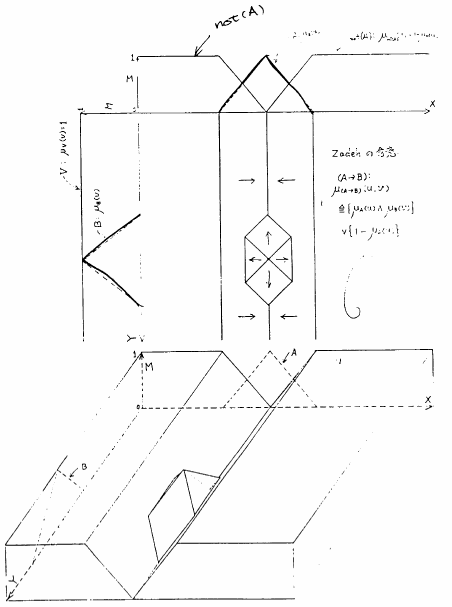
 の実際のメンバシップ関数には,バリエーションが存在すると解釈した方がすっきりする.).ここで例として,
の実際のメンバシップ関数には,バリエーションが存在すると解釈した方がすっきりする.).ここで例として,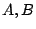 が共に単項ファジィ関係即ちファジィ集合として三角型のメンバシップ関数で与えられた場合の
が共に単項ファジィ関係即ちファジィ集合として三角型のメンバシップ関数で与えられた場合の
 のメンバシップ関数を図5.4に図示する.図中で,半分隠れているピラミッド型の部分が
のメンバシップ関数を図5.4に図示する.図中で,半分隠れているピラミッド型の部分が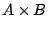 のメンバシップ関数,高原とV次谷の部分がnot(
のメンバシップ関数,高原とV次谷の部分がnot( )
)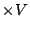 のメンバシップ関数となっている.このように見ると,
のメンバシップ関数となっている.このように見ると,
 のグレードは,「
のグレードは,「 のグレードも
のグレードも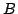 のグレードも大きいとき」かまたは「
のグレードも大きいとき」かまたは「 のグレードが小さい(即ちnot(
のグレードが小さい(即ちnot( )のグレードが大きい)とき」に大きくなる.言い替えると,「前件部
)のグレードが大きい)とき」に大きくなる.言い替えると,「前件部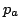 も後件部
も後件部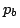 も真に近いとき」かまたは「前件部
も真に近いとき」かまたは「前件部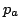 が偽に近いとき」に
が偽に近いとき」に
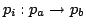 は真に近くなる.これは,通常の含意命題の自然な拡張になっているのがわかる.事実,Zadehのファジィ含意は(どの
は真に近くなる.これは,通常の含意命題の自然な拡張になっているのがわかる.事実,Zadehのファジィ含意は(どの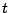 - ノルム,
- ノルム, - ノルムを用いようとも)通常の含意の拡張になっており,
- ノルムを用いようとも)通常の含意の拡張になっており, をクリスプ集合とすれば,前項で述べた通常の含意の真理値表と一致することは容易に確かめられる.
をクリスプ集合とすれば,前項で述べた通常の含意の真理値表と一致することは容易に確かめられる.
図 5.4
Zadehによるファジィ含意命題の

 |
このZadehのファジィ含意は,5.3節で説明するファジィ推論の基本規則に基づけば自然に導出されるものである.ここで,その概略を述べると以下のようになる.即ち,ファジィ含意 は,「
は,「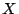 が
が ならば
ならば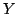 は
は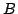 である」を意味するのだが,もう少し詳しく考えると「
である」を意味するのだが,もう少し詳しく考えると「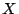 が
が でないならば
でないならば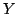 は何かわからない」ということを暗に主張している.したがって,
は何かわからない」ということを暗に主張している.したがって,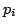 は「
は「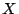 が
が でかつ
でかつ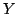 が
が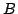 であるか,または,
であるか,または,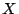 が
が ではなくかつ
ではなくかつ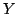 が不定である」と読み変えることができる.ここで,「
が不定である」と読み変えることができる.ここで,「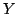 が不定である」ということは,
が不定である」ということは,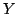 がその定義域
がその定義域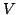 のどの要素でも値としてとりうるということだからこれは「
のどの要素でも値としてとりうるということだからこれは「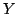 は
は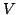 である」ということに他ならない.したがって
である」ということに他ならない.したがって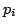 は,
は,
と表現される.ここで,5.3節で説明するように,
となるから,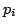 は結局,
は結局,
となり,zadehのファジィ含意における
 が得られる.
Zadehの提案した
が得られる.
Zadehの提案した
 の定義の他に,よく用いられるのが,Lukasiewiczの連続値論理における含意と整合した
の定義の他に,よく用いられるのが,Lukasiewiczの連続値論理における含意と整合した
 の定義である.Lukasiewiczの定義によると,
の定義である.Lukasiewiczの定義によると,
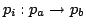 の真理値
の真理値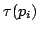 は,前件部と後件部の真理値
は,前件部と後件部の真理値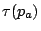 と
と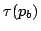 とによって
とによって
と定義される.これも通常の含意命題の拡張となっていることは容易に理解される.
ここで,ファジィ命題においては,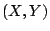 の値が
の値が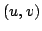 のとき
のとき
だから,これを,上のLukasiewiczの含意の定義にそのまま適用すれば,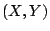 が
が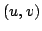 のときのファジィ含意命題
のときのファジィ含意命題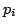 の真理値は,
の真理値は,
と与えられる.ここでこの真理値は
 の
の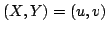 におけるグレードに他ならないから,結局,Lukasiewiczの含意に従う限り
におけるグレードに他ならないから,結局,Lukasiewiczの含意に従う限り
 のメンバシップ関数は,
のメンバシップ関数は,
と定義される.
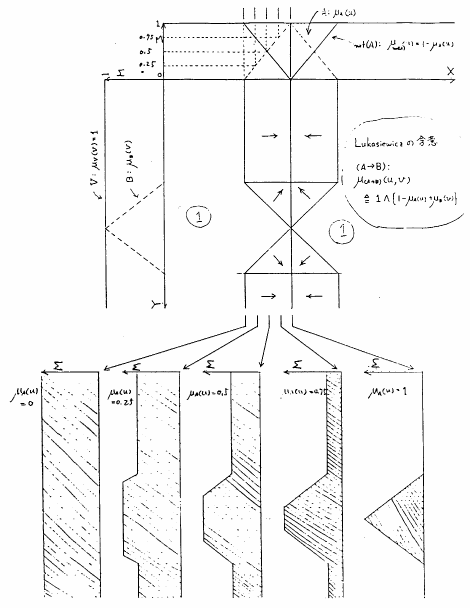
ここで例として, が共に単項ファジィ関係即ちファジィ集合として三角型のメンバシップ関数で与えられた場合の,Lukasiewiczの含意に基づく
が共に単項ファジィ関係即ちファジィ集合として三角型のメンバシップ関数で与えられた場合の,Lukasiewiczの含意に基づく
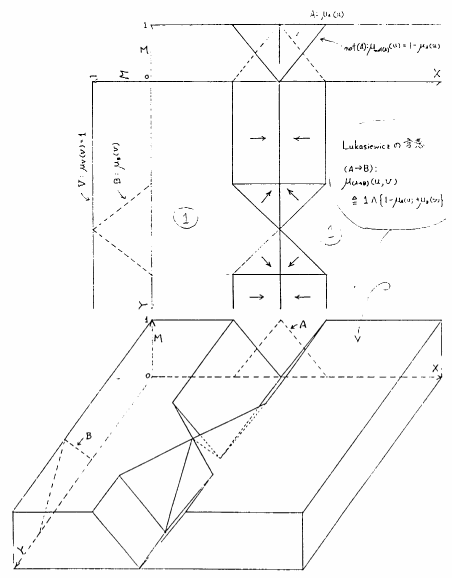
 のメンバシップ関数を図5.5に示す.
のメンバシップ関数を図5.5に示す.
図 5.5
Lukasiewiczによるファジィ含意命題の

 |
ファジィ制御などで,最も,多く使われているファジィ含意として,Mandaniによって提案されたものがある.これによると,
と定義される.これは,つまり, - ノルムに論理積を選んだ場合の
- ノルムに論理積を選んだ場合の と
と の直積のメンバシップ関数にならず,Mandaniの含意では,
の直積のメンバシップ関数にならず,Mandaniの含意では,
であると考えてよい.むしろ,これがMandaniの含意の一般的な定義と考えた方がよく,直積の定義(あるいは,その基となる,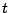 - ノルムの選び方)によって,
- ノルムの選び方)によって,
 の実際のメンバシップ関数には,いろいろなバリエーションが存在する.
ここで例として,
の実際のメンバシップ関数には,いろいろなバリエーションが存在する.
ここで例として, が共に単項ファジィ関係即ちファジィ集合として三角型のメンバシップ関数で与えられた場合のMandaniの含意に基づく
が共に単項ファジィ関係即ちファジィ集合として三角型のメンバシップ関数で与えられた場合のMandaniの含意に基づく
 のメンバシップ関数を図5.6に示す.
のメンバシップ関数を図5.6に示す.
図 5.6
Mandaniによるファジィ含意命題の

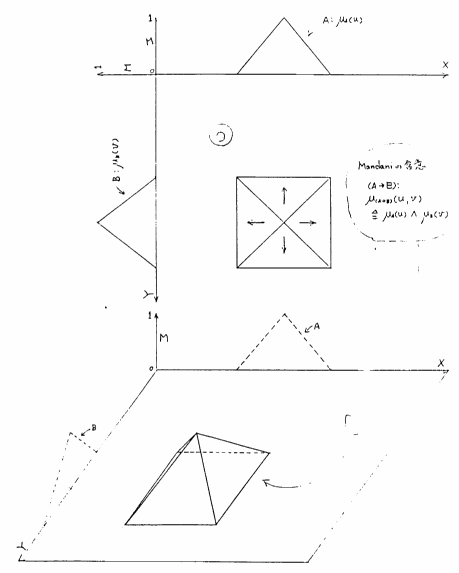 |
一見してわかるように,Mandaniの含意は,ZadehやLukasiewiczの含意とかなり様子が違う.これでは,
 も
も
 も同じになってしまい,方向性がみられない.また事実,これは,通常の含意命題の拡張とはなっていない.
しかし,Mandaniの含意とZadehの含意の
も同じになってしまい,方向性がみられない.また事実,これは,通常の含意命題の拡張とはなっていない.
しかし,Mandaniの含意とZadehの含意の
 を見比べてみるとMandaniの含意は,Zadehの含意の前半の部分であることに気づく.つまり,Zadehの定義では,「
を見比べてみるとMandaniの含意は,Zadehの含意の前半の部分であることに気づく.つまり,Zadehの定義では,「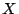 が
が ならば
ならば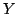 は
は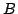 」が主張されたとき「
」が主張されたとき「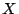 が
が でなければ
でなければ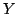 は不定」が暗黙に主張されるものとして
は不定」が暗黙に主張されるものとして
 を定義したが(実は,通常の含意も同様である.)Mandaniの定義は「
を定義したが(実は,通常の含意も同様である.)Mandaniの定義は「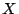 が
が ならば
ならば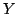 は
は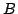 」だけを定義し,「
」だけを定義し,「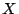 が
が でない場合」に対しては,定義を与えていない.あるいは,言い替えると「
でない場合」に対しては,定義を与えていない.あるいは,言い替えると「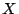 が
が ならば
ならば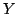 は
は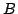 」で「
」で「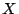 が
が でなければ
でなければ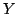 は定義されない」と定義しているともみなせる.
逆の見方をすると,Zadehの定義における
は定義されない」と定義しているともみなせる.
逆の見方をすると,Zadehの定義における
 は,Mandaniの定義における
は,Mandaniの定義における
 と
と
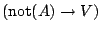 をコンポーネントとして,これらの和集合をとったものと考えることもできる.
ファジィ含意の定義としては,多用なものが提案されているが,主に用いられるのは,本節で上に述べられた3種である(その他についての詳細は,文献[M-4]などを参照されたい).
Zadehの含意とLukasiewiczの含意はともに,通常の含意の拡張となっており,
をコンポーネントとして,これらの和集合をとったものと考えることもできる.
ファジィ含意の定義としては,多用なものが提案されているが,主に用いられるのは,本節で上に述べられた3種である(その他についての詳細は,文献[M-4]などを参照されたい).
Zadehの含意とLukasiewiczの含意はともに,通常の含意の拡張となっており, と
と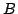 をクリスプ集合とすればどちらの含意で定義しようとも
をクリスプ集合とすればどちらの含意で定義しようとも
 は結果的に同じになり,しかもこれは,通常の含意命題の定義とも一致する.
は結果的に同じになり,しかもこれは,通常の含意命題の定義とも一致する. または
または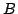 がファジィ関係の場合は,このふたつの含意に違いが現われるが,大局的には,似た傾向が見られる.図5.7,図5.8のように,
がファジィ関係の場合は,このふたつの含意に違いが現われるが,大局的には,似た傾向が見られる.図5.7,図5.8のように,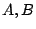 がファジィ集合の場合の,それぞれの含意による
がファジィ集合の場合の,それぞれの含意による
 のメンバシップ関数のいくつかの断面を,前件部
のメンバシップ関数のいくつかの断面を,前件部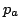 の真理値(つまり,
の真理値(つまり,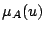 )をパラメータとして図示してみると,共に(途中の変化の仕方に違いがあるにしても),前件部の真理値が高いとき後件部の主張が支配的となり,逆に,前件部の真理値が低いとき含意命題の主張が不定に近づく様子が見て取れる.ここで,Zadehの含意はファジィ理論から直接に導出されるものであるのに対し,Lukasiewiczの含意はもともとファジィ理論とは関係なく定義されていることに注意する.
)をパラメータとして図示してみると,共に(途中の変化の仕方に違いがあるにしても),前件部の真理値が高いとき後件部の主張が支配的となり,逆に,前件部の真理値が低いとき含意命題の主張が不定に近づく様子が見て取れる.ここで,Zadehの含意はファジィ理論から直接に導出されるものであるのに対し,Lukasiewiczの含意はもともとファジィ理論とは関係なく定義されていることに注意する.
図 5.7
Zadehによる
 の断面
の断面
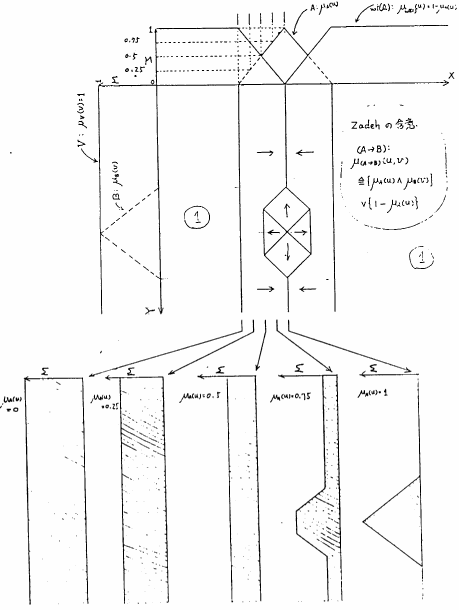 |
図 5.8
Lukasiewiczによる
 の断面
の断面
 |
Mandaniの含意は,図5.9の断面を見てもわかるように,先の2つとは趣を異にしており,通常の含意の拡張ともなっていない.同図では,前件部の真理値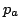 (つまり
(つまり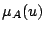 )が0の場合,この含意命題の真理値は常に0となっている.これは,つまり,前件部が偽なら後件部は常に偽即ち後件部変数はどのような値をとる可能性もないことを表している.このように,Mandaniの含意は異質のような感じを受けるが,これを,基礎となる論理系を基に考えると,Mandaniの含意は,Zadehの含意と本質的に同質のものであると考えることができる.Zadehの含意では,「
)が0の場合,この含意命題の真理値は常に0となっている.これは,つまり,前件部が偽なら後件部は常に偽即ち後件部変数はどのような値をとる可能性もないことを表している.このように,Mandaniの含意は異質のような感じを受けるが,これを,基礎となる論理系を基に考えると,Mandaniの含意は,Zadehの含意と本質的に同質のものであると考えることができる.Zadehの含意では,「 が
が 」である場合と,「
」である場合と,「 が
が でない」場合の両方に対して定義を与えているが,Mandaniの含意では,「
でない」場合の両方に対して定義を与えているが,Mandaniの含意では,「 が
が 」の場合だけを定義しているところに違いがある.また,Zadehの含意は,Mandaniの含意をコンポーネントとして,それらの組合せでできていると考えることもできる.
」の場合だけを定義しているところに違いがある.また,Zadehの含意は,Mandaniの含意をコンポーネントとして,それらの組合せでできていると考えることもできる.
図 5.9
Mandaniによる
 の断面
の断面
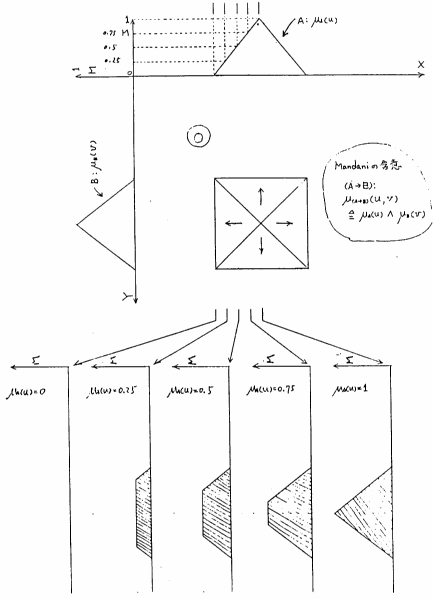 |
実際のファジィ制御では,Mandaniの含意が圧倒的に多く用いられている.それは,Mandaniの含意が最も簡単なものであり,しかも,本質的にそれがコンポーネントとしての性質を持っているため,複数の含意(複数の制御規則に対応する)を扱う場合にその取り扱いが容易になるためである(5.4節参照).Mandaniの含意を組み合わせて,規則「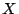 が
が ならば
ならば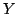 は
は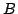 」の適用されない場合(ここでは「
」の適用されない場合(ここでは「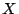 が
が でない」の場合)に対して,意図的に「
でない」の場合)に対して,意図的に「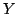 は不定である」という情報を付け加えて,Zadehの含意を構成することも可能だが,通常のMandaniの含意を用いた応用システムではこの処理は行われず,結果的に,規則が適用されない場合は「
は不定である」という情報を付け加えて,Zadehの含意を構成することも可能だが,通常のMandaniの含意を用いた応用システムではこの処理は行われず,結果的に,規則が適用されない場合は「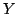 は定義されない」と定義されることになる.しかし,これは,ファジィ制御においては,不都合ではない場合が多い.つまり,うまく合致する規則がない場合に,制御量が不定(何であってもよい)と推論されるよりは,適当な制御量が定義されないと推論される方が安全な場合があるからだ.さらにいえば,結果として推論されるファジィ集合からさらにある代表値を重心として選び出し,それを推論された制御パラメータとして採用する場合には,規則の合致しない場合の処理は結果にあまり影響しないだろうと推論される.つまり,規則の合致しない場合を「不定」としようと「定義されない」としようと重心の位置の変化にあまり影響を与えないだろうことが,図5.7と図5.9の比較から推察されるだろう.
は定義されない」と定義されることになる.しかし,これは,ファジィ制御においては,不都合ではない場合が多い.つまり,うまく合致する規則がない場合に,制御量が不定(何であってもよい)と推論されるよりは,適当な制御量が定義されないと推論される方が安全な場合があるからだ.さらにいえば,結果として推論されるファジィ集合からさらにある代表値を重心として選び出し,それを推論された制御パラメータとして採用する場合には,規則の合致しない場合の処理は結果にあまり影響しないだろうと推論される.つまり,規則の合致しない場合を「不定」としようと「定義されない」としようと重心の位置の変化にあまり影響を与えないだろうことが,図5.7と図5.9の比較から推察されるだろう.



: ファジィ推論
: ファジィ推論の数学的解釈
: ファジィ命題とその標準形
目次
平成12年5月17日
![]() の真理値は,
の真理値は,![]() が真のときは
が真のときは![]() の真理値に従い,
の真理値に従い,![]() が偽のときは常に真となっている.ここで,「
が偽のときは常に真となっている.ここで,「![]() が真のとき」というのは「
が真のとき」というのは「![]() の値
の値![]() が
が![]() を満たすとき」であり「
を満たすとき」であり「![]() が偽のとき」というのは,「
が偽のとき」というのは,「![]() の値
の値![]() が
が![]() を満たすとき」であることに注意し,さらに
を満たすとき」であることに注意し,さらに![]() の値が
の値が![]() であるときの
であるときの![]() の真理値
の真理値![]() は
は![]() となることに注意すれば,
となることに注意すれば,![]() に対する
に対する![]() の真理値
の真理値![]() は,
は,