


: 結言
: ファジィ理論の図形,画像分野における応用例
: ファジィ・クラスタリング
目次
寺野らによって提案されている農産物の形状認識はファジィ推論技術を駆使した図形の認識技術として興味深いものである.ここでは「農産物の形状」という本質的に曖昧にしか定義されないものを基準にして農産物の名前を推論するという正にファジィ推論ならではの問題を扱っている.
推論は基本的に2段階に分けられる.ひとつは,得られた画像データから輪郭線の局所的な特徴を認識する部分である.もうひとつは,第1段階で得られた輪郭線の局所的な特徴とその他の特徴を手がかりとして,入力データと農産物の標準データと比較し,農産物名を推論する部分である.それぞれの部分でファジィ推論技術が応用されている.
まず入力された画像データから適当な前処理を行った後,輪郭線が抽出される.次に,この輪郭線は一定長の短い線分に区切られ,隣接する線分との角度差が調べられる.そして,角度差の変化が10度以内の線分をまとめてグルーピングする.例えば,図6.3のような場合は,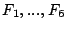 の6つにグルーピングされる.これは,つまり,曲率の変化がある程度以上大きいところで分割していると考えてもよい.次に各々のグループの直線らしさ,曲線らしさ,角らしさがファジィ推論によって推論され,これが,輪郭線の局所的な特徴となる.この局所的な特徴の推論は以下のように行われる.
の6つにグルーピングされる.これは,つまり,曲率の変化がある程度以上大きいところで分割していると考えてもよい.次に各々のグループの直線らしさ,曲線らしさ,角らしさがファジィ推論によって推論され,これが,輪郭線の局所的な特徴となる.この局所的な特徴の推論は以下のように行われる.
図 6.3
輪郭線のグルーピングの例
|
|
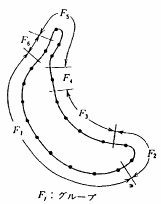
まず,直線,曲線,角の概念は,平均の角度差(平均の曲率に対応)の全体を台集合とするファジィ集合として,図6.4のように予め定義されているものとする.即ち例えば「グループ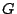 は曲線である」という命題は,グループ
は曲線である」という命題は,グループ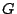 の平均角度差を表す変数を
の平均角度差を表す変数を とすれば,
とすれば,

is
となる.
図 6.4
直線,曲線,角のメンバシップ関数
|
|
さらに,実際に得られた輪郭データのあるグループ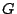 の角度差が観測されたとき,この事実は,その
の角度差が観測されたとき,この事実は,その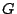 内の角度差の平均を頂点として,偏差をあいまい幅とするような二等辺三角形をメンバシップ関数とするファジィ集合
内の角度差の平均を頂点として,偏差をあいまい幅とするような二等辺三角形をメンバシップ関数とするファジィ集合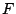 を用いて,
を用いて,

is
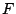
という命題で表されるものとする.
ここで,例えば,あるグループ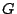 が観測されたとき,この
が観測されたとき,この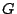 がどの程度「曲線」であるといえるかを推論すればよいのであるが,これは,
となるような
がどの程度「曲線」であるといえるかを推論すればよいのであるが,これは,
となるような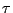 を求める問題に他ならない.このような問題は,5.5節で述べた真理値限定の逆の操作にあたり逆真理値限定法と呼ばれる.このような
を求める問題に他ならない.このような問題は,5.5節で述べた真理値限定の逆の操作にあたり逆真理値限定法と呼ばれる.このような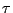 は一般にタイプ2ファジィ集合となるが,塚本の提案した数値的真理値による逆真理値限定法を用いれば,
は一般にタイプ2ファジィ集合となるが,塚本の提案した数値的真理値による逆真理値限定法を用いれば,
と,区間![$[0,1]$](img106.gif) の間のある実数として,その真理値を推定することができる(注意:本報告では,詳しくのべる余裕がないが,上の真理値は「
の間のある実数として,その真理値を推定することができる(注意:本報告では,詳しくのべる余裕がないが,上の真理値は「 が
が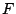 であるとき
であるとき が
が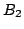 である可能性と
である可能性と が
が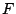 でないときに
でないときに が
が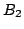 でない必然性の平均」を与えていることが様相性の議論から明らかになる.).
このような逆真理値限定を用いて図6.3の
でない必然性の平均」を与えていることが様相性の議論から明らかになる.).
このような逆真理値限定を用いて図6.3の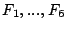 の各々の直線,曲線,角らしさを求めれば,表6.1のような結果が得られ,局所的な輪郭形状の特徴がグループごとに推論される.ただし,表6.1の曲線の真理値の符号は単に凸であるか凹であるかの区別を表している.
の各々の直線,曲線,角らしさを求めれば,表6.1のような結果が得られ,局所的な輪郭形状の特徴がグループごとに推論される.ただし,表6.1の曲線の真理値の符号は単に凸であるか凹であるかの区別を表している.
表 6.1
輪郭線の局所的特徴の認識結果の例
| グループ |
グループの長さ |
直線 |
曲線 |
角 |
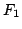 |
9 |
0 |
0.71 |
0 |
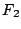 |
2 |
0 |
0 |
1.0 |
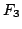 |
4 |
0 |
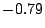 |
0 |
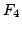 |
1 |
0.43 |
0.02 |
0 |
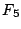 |
3 |
0 |
0 |
0.78 |
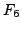 |
1 |
0 |
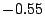 |
0 |
前項とは別に,マクロな標準図形として,円,楕円,三角,四角,棒,弓形の6つの図形を選び,マクロな形状がこの標準図形のどれかであることをファジィ命題で表す.このため,「縦横比」,「曲線の割合」,「角の数」,「凸部の割合」,「凹部の割合」の5つを要素とする5次元変数「マクロ形状」を導入し,それぞれの標準図形を適当な5項ファジィ関係によって定義する.
例えば,「マクロ形状が円である」という命題は,
| |
「縦横比」 |
is |
「1に近い」 |
| and |
「曲線の割合」 |
is |
「大半」 |
| and |
「角の数」 |
is |
「0に近いかだいたい6より多い」 |
| and |
「凸部の割合」 |
is |
「ほとんど100%」 |
| and |
「凹部の割合」 |
is |
「ほとんど0%」 |
と5つのファジィ命題の統合により表すことができ,ここで,5.2節の直積を用いれば,
「マクロ形状」=(「縦横比」,「曲線の割合」,「角の数」,「凸部の割合」,「凹の割合」)
なる5次元の変数と
「円」=「1に近い」×「大半」×「0に近いかだいたい6より多い」×「ほとんど100%」×「ほとんど0%」
なる5項ファジィ関係を用いて,
「マクロ形状」 is 「円」
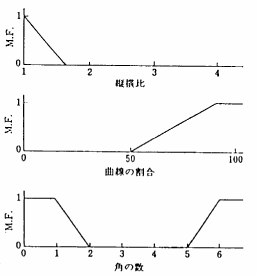
とさらに簡単に表記される.ここで「1に近い」,「大半」,「0に近いかだいたい6より多い」などのファジィ集合は,図6.5のように与えられる.
図 6.5
「1に近い」,「大半」,「0に近いかだいたい6より多い」のメンバシップ関数
|
|
同様にして,残りの標準図形に対して適当な5項ファジィ関係「楕円」,「三角」,「四角」,「棒」,「弓形」を定義すればそれぞれの基本図形の形状は,
「マクロ形状」 is 「楕円」
「マクロ形状」 is 「三角」
「マクロ形状」 is 「四角」
「マクロ形状」 is 「棒」
「マクロ形状」 is 「弓形」
なる命題で表現される.
前項のように標準図形のマクロ形状が定義されると,農産物のマクロ形状のような数値的に表しにくい形状でも,標準図形のマクロ形状の組み合わせとして,容易に定義することができる.例えば,バナナの形は棒のような形か弓のような形をしていると考えられるから,バナナのマクロ形状を与える5項ファジィ関係:「バナナ形」は,
「バナナ形」=「棒」∪「弓形」
と,標準図形のマクロ形状を定義する5項ファジィ関係の演算によって容易に計算される.これを用いると「マクロ形状がバナナ形をしている」という命題は,
「マクロ形状」 is 「バナナ形」
と表現される.
農産物の定義をあたえる変数としては「マクロ形状」の他に,新たに
「大きさ」=(「面積」,「長さ」)
「凸凹」
なる変数を導入し,
「農産物」
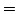
(「大きさ」,「マクロ形状」,「凸凹」)
なる7次元の変数を用いれば,これに対応した7項ファジィ関係によって農産物の定義が与えられる.例えば,バナナを定義する7項ファジィ関係:「バナナ」は,
と与えることができ,これにより「農産物はバナナである」という命題は,
「農産物」 is 「バナナ」
と標準形で表現することができる.
同様にして,他の農産物を定義する7項ファジィ関係を与えておけば,それぞれの農産物であるという命題はすべて上と同型の標準命題で表されることになる.
実際にある物体の輪郭が観測されたら,その物体に対する,7次元変数:「農産物」の値を計算する.このとき,「面積」,「長さ」,「縦横比」の値は観測データから直接的に求められる.その他の変数の値に関しては,表6.1のような輪郭線の局所的特徴の推論結果から求める.
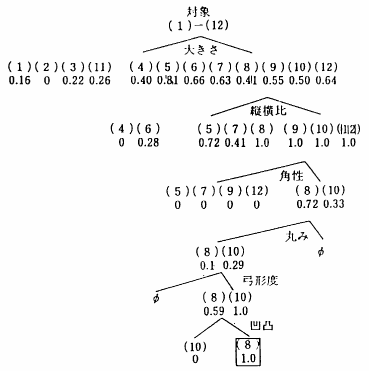
さて観測物体の「農産物」の値がわかれば,推論法1のようにして,それぞれの農産物を定義する7項ファジィ関係との適合度が計算され,結局,最も大きな適合度の得られた,農産物が認識結果として得られる.図6.7は図6.6のような候補群から,ピーマンを認識した例を示している.
図 6.6
入力図形の例
 |
図 6.7
ピーマンの認識例
 |
この農産物の形状認識では,逆真理値限定法と,通常のファジィ推論法1を巧みに組み合わせて用いており,ファジィ推論の図形認識における応用を考える上では,示唆に富んだものとなっている.特に画像データそのものに直接的にファジィ推論を用いることを避け,予め,ある程度大きな単位にグループ分けしたものを対象に逆真理値限定を用いて「直線」,「曲線」,「角」などの言語的なラベル付けをするところが興味深い.これは単に計算量を減らしているばかりではなく,言語という本来あるまとまった対象に対する概念を誘導するものと観測データとの整合をとるという本質的な役割を果たしている.



: 結言
: ファジィ理論の図形,画像分野における応用例
: ファジィ・クラスタリング
目次
平成12年5月17日