


: 確率限定の実例
: ファジィ命題の確率限定
: ファジィ命題の確率限定
目次
「( is
is 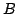 )がほとんどの場合に真である」というような命題を確率限定命題といい,この命題の真偽値を求める問題はファジィ命題の確率限定と呼ばれる.ここで,
)がほとんどの場合に真である」というような命題を確率限定命題といい,この命題の真偽値を求める問題はファジィ命題の確率限定と呼ばれる.ここで,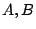 は共にファジィ集合であり,特に
は共にファジィ集合であり,特に が変数ではないことに注意する.例えば
が変数ではないことに注意する.例えば が「日本人」を表すファジィ集合で,
が「日本人」を表すファジィ集合で,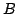 が「黒髪の人」という概念を表すファジィ集合とすれば,「日本人は黒髪だということはほとんどの場合に真である」というような命題が確率限定命題となる.
この確率限定命題をZadeh流に表記すると,
が「黒髪の人」という概念を表すファジィ集合とすれば,「日本人は黒髪だということはほとんどの場合に真である」というような命題が確率限定命題となる.
この確率限定命題をZadeh流に表記すると,
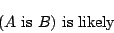 |
(3.1) |
となる.ここで,likelyが限定ファジィ確率である.
またこの確率限定命題は次のような形の「傾向命題」に書き換えることができる.
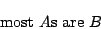 |
(3.2) |
これは,先の例では,「ほとんどの日本人は黒髪だ」と言い換えたことにあたる.ここで式(3.2)のmostは「ファジィ限量作用素」と呼ばれるものである.
ただし,ここで,式(3.1)と式(3.2)が同値な命題を示すと思うためには,当然のことながらlikelyとmostが数値的に等しい概念を表しているという暗黙の了解がなされている必要がある.一般に,確率限定命題と傾向命題は数値的に同等な限定ファジィ確率とファジィ限量作用素を用いれば互いに置き換えが可能であることがわかるから,これらを表すファジィ数を一般に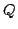 (
(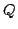 は
は![$[0,1]$](img15.gif) を台集合とするファジィ数)とおけば,確率限定命題も傾向命題も式(3.2)の一般化として,
を台集合とするファジィ数)とおけば,確率限定命題も傾向命題も式(3.2)の一般化として,
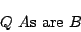 |
(3.3) |
と表現される.例えば,ファジィ限量作用素がmost(限定ファジィ確率としてはlikely)の場合は1に近い方に分布のかたまったファジィ数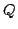 (これは,ちょうど,真理値限定における「真」のファジィ真理値と同じようなものとなるだろう)を定義し,また逆にファジィ限量作用素がfew(限定ファジィ確率としてはunlikely)の場合は0に近い方に分布のかたまったファジィ数
(これは,ちょうど,真理値限定における「真」のファジィ真理値と同じようなものとなるだろう)を定義し,また逆にファジィ限量作用素がfew(限定ファジィ確率としてはunlikely)の場合は0に近い方に分布のかたまったファジィ数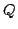 (「偽」のファジィ真理値に対応)を定義して用いればよい.
結局,問題は,式(3.3)の形で表現された傾向命題の真偽値を求めることに帰着されるのであるが,式(3.3)は,相対シグマカウントという概念を導入することにより,さらに,
(「偽」のファジィ真理値に対応)を定義して用いればよい.
結局,問題は,式(3.3)の形で表現された傾向命題の真偽値を求めることに帰着されるのであるが,式(3.3)は,相対シグマカウントという概念を導入することにより,さらに,
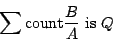 |
(3.4) |
と解釈される.ただし,
 は「
は「 における
における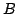 の相対シグマカウント」と呼ばれるもので,
の相対シグマカウント」と呼ばれるもので,
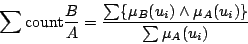 |
(3.5) |
と定義されている.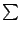 はすべての
はすべての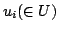 に対しての総和をとることを意味する.
ここで,あるファジィ集合
に対しての総和をとることを意味する.
ここで,あるファジィ集合 に対する値
に対する値
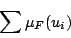 |
(3.6) |
は の各要素のグレードをすべて足し合わせたものであり,ファジィ集合
の各要素のグレードをすべて足し合わせたものであり,ファジィ集合 の「濃度」と呼ばれるものである.これは,離散的なクリスプ集合の通常の濃度に対応するものであり,その拡張となっている.離散的なクリスプ集合の濃度は結局その集合の中に含まれる要素の個数を表していることに他ならないのであるが,この意味からすると,ファジィ集合の濃度はそのファジィ集合に含まれる要素の(それぞれの要素は含まれているかどうか二値的には判断されないにもかかわらず)等価的な個数を表していると考えられる.
以上のように考えると式(3.5)の相対シグマカウントは,ファジィ集合
の「濃度」と呼ばれるものである.これは,離散的なクリスプ集合の通常の濃度に対応するものであり,その拡張となっている.離散的なクリスプ集合の濃度は結局その集合の中に含まれる要素の個数を表していることに他ならないのであるが,この意味からすると,ファジィ集合の濃度はそのファジィ集合に含まれる要素の(それぞれの要素は含まれているかどうか二値的には判断されないにもかかわらず)等価的な個数を表していると考えられる.
以上のように考えると式(3.5)の相対シグマカウントは,ファジィ集合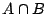 の濃度のファジィ集合
の濃度のファジィ集合 の濃度に対する比を表していると考えられる.即ち「
の濃度に対する比を表していると考えられる.即ち「 」である場合(要素)の数に対して「
」である場合(要素)の数に対して「 でしかも
でしかも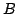 」である場合(要素)の数の比率がどのくらいであるかを区間
」である場合(要素)の数の比率がどのくらいであるかを区間![$[0,1]$](img15.gif) の中のある実数で表していることになる.そして,この比率が1に近いということは(
の中のある実数で表していることになる.そして,この比率が1に近いということは( is
is 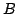 )が起こりやすいことを示し,0に近いということは起こりにくいことを示していることになる.
式(3.4)の命題は,結局,この比率がファジィ数
)が起こりやすいことを示し,0に近いということは起こりにくいことを示していることになる.
式(3.4)の命題は,結局,この比率がファジィ数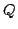 であることを主張していることになるが,これが意味的に式(3.3)の置き換えとなることは頷けるであろう.ここで,式(3.4)の真偽値は,式(3.5)の相対シグマカウントの値から,
であることを主張していることになるが,これが意味的に式(3.3)の置き換えとなることは頷けるであろう.ここで,式(3.4)の真偽値は,式(3.5)の相対シグマカウントの値から,
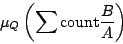 |
(3.7) |
と容易に計算され,これが即ち,式(3.3)の傾向命題(あるいはこれと等価な確率限定命題)の真偽値となる.



: 確率限定の実例
: ファジィ命題の確率限定
: ファジィ命題の確率限定
目次
平成12年5月17日