


: 様相論理
: ファジィ論理と種々の論理体系
: 古典論理
目次
上で述べた,古典論理は2値論理即ち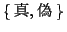 だけを扱っているぶんには問題は無い.しかし,例えば「この命題は偽である」という命題のように,「真」とも「偽」ともそのどちらともいえない命題を,どのように扱えばよいかという問題が出てきた.このような問題に対して,第3の真理値として,「不定」を導入した3値論理が提案され,さらにその一般化として多値論理が提案された.これは,とりも直さず,命題には真でも偽でもないものが存在することを認めることであるが,これは式(4.9)の排中律を否定,つまり古典論理を否定することになる.排中律「
だけを扱っているぶんには問題は無い.しかし,例えば「この命題は偽である」という命題のように,「真」とも「偽」ともそのどちらともいえない命題を,どのように扱えばよいかという問題が出てきた.このような問題に対して,第3の真理値として,「不定」を導入した3値論理が提案され,さらにその一般化として多値論理が提案された.これは,とりも直さず,命題には真でも偽でもないものが存在することを認めることであるが,これは式(4.9)の排中律を否定,つまり古典論理を否定することになる.排中律「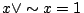 」が意味的に「命題
」が意味的に「命題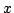 または命題
または命題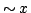 のどちらかが真(1)である」つまり,「
のどちらかが真(1)である」つまり,「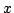 であるかまたは
であるかまたは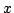 でないかのどちらかである」ことを表していることから明らかであろう.
もともと古典論理では,集合論やそれらに用いられる論理などをすべて公理化し,その上でその体系から矛盾が起こらないことを証明すればよい」という立場を取っている.こういう立場からすれば上の問題に対しては,真理値「不定」を導入する公理を付加してもっと強力な公理体系をつくることにより,その体系内の矛盾が無くなるようにすればよい.しかしこのような強化された体系でも「この命題は真か不定かであるということは偽である」という命題の真理値を定めることはできないことはすぐにわかる.
一般に,「現在の算術の公理系を含む無矛盾な公理系は不完全である.即ち,その公理系の算術命題でその公理系の中では肯定も否定もできないものが存在する.」という「ゲーテの不完全性定理」が証明されている.これは,古典論的な無矛盾な公理系による論理では証明のできない命題が必ず存在することを示している(これは必ずしも古典論理を否定するものではなく,古典論理で証明できる命題には限度があることをいっているにすぎない.).
ここから,Browerにより,直観主義の立場,即ち,具体的に明らかな概念から一歩一歩具体的に構成してゆく限り矛盾は起こりようがないという立場からの論理,「直観主義論理」が展開されるようになった.
この直観主義論理では,命題が真であることも偽であることも証明できないことがあることを積極的に認め,ある命題が真であることを証明するためには具体的にそれが真であることを構成的に導かなくてはならないという立場に立っている.つまりある命題を認めるということは,その命題を確かめる,ある構成的な具体的な方法を持っているということで,このとき,その命題は「証明可能」であるという.したがって,「
でないかのどちらかである」ことを表していることから明らかであろう.
もともと古典論理では,集合論やそれらに用いられる論理などをすべて公理化し,その上でその体系から矛盾が起こらないことを証明すればよい」という立場を取っている.こういう立場からすれば上の問題に対しては,真理値「不定」を導入する公理を付加してもっと強力な公理体系をつくることにより,その体系内の矛盾が無くなるようにすればよい.しかしこのような強化された体系でも「この命題は真か不定かであるということは偽である」という命題の真理値を定めることはできないことはすぐにわかる.
一般に,「現在の算術の公理系を含む無矛盾な公理系は不完全である.即ち,その公理系の算術命題でその公理系の中では肯定も否定もできないものが存在する.」という「ゲーテの不完全性定理」が証明されている.これは,古典論的な無矛盾な公理系による論理では証明のできない命題が必ず存在することを示している(これは必ずしも古典論理を否定するものではなく,古典論理で証明できる命題には限度があることをいっているにすぎない.).
ここから,Browerにより,直観主義の立場,即ち,具体的に明らかな概念から一歩一歩具体的に構成してゆく限り矛盾は起こりようがないという立場からの論理,「直観主義論理」が展開されるようになった.
この直観主義論理では,命題が真であることも偽であることも証明できないことがあることを積極的に認め,ある命題が真であることを証明するためには具体的にそれが真であることを構成的に導かなくてはならないという立場に立っている.つまりある命題を認めるということは,その命題を確かめる,ある構成的な具体的な方法を持っているということで,このとき,その命題は「証明可能」であるという.したがって,「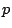 ではないことはない」つまり「
ではないことはない」つまり「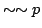 」を証明しても,それは「
」を証明しても,それは「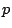 である」ことを証明したことにはならない.これは古典論理で成立している式(4.12)のような2重否定の性質を認めないことであり,直観主義論理では「背理法」は成立しないことを意味する.また当然,式(4.9)の排中律も直観主義論理では認めない,
では,つぎに,この直観主義論理における真理値の集合としてどのような構造が必要となるかを説明し,その論理演算がどのように定義されるかを具体的に説明する.
直観主義論理の真理値集合の数学的構造モデルとしては,「完備ハイティング代数(complete Heyting algebra,略してcHa)」が仮定される.ここで,cHaは完備束の特別な場合であり,完備束
である」ことを証明したことにはならない.これは古典論理で成立している式(4.12)のような2重否定の性質を認めないことであり,直観主義論理では「背理法」は成立しないことを意味する.また当然,式(4.9)の排中律も直観主義論理では認めない,
では,つぎに,この直観主義論理における真理値の集合としてどのような構造が必要となるかを説明し,その論理演算がどのように定義されるかを具体的に説明する.
直観主義論理の真理値集合の数学的構造モデルとしては,「完備ハイティング代数(complete Heyting algebra,略してcHa)」が仮定される.ここで,cHaは完備束の特別な場合であり,完備束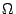 の任意の要素
の任意の要素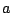 と任意の
と任意の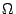 の部分集合
の部分集合
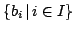 に対して,
に対して,
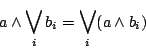 |
(4.13) |
なる条件が成立するとき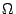 はcHaであるという.cHaを仮定するのは,次のような直観主義論理における含意演算(
はcHaであるという.cHaを仮定するのは,次のような直観主義論理における含意演算(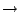 )の定義を可能とするためである.
直観主義論理では,構成的な証明だけが証明としての意味を持つため,構成的な論理演算である含意演算(
)の定義を可能とするためである.
直観主義論理では,構成的な証明だけが証明としての意味を持つため,構成的な論理演算である含意演算(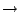 )の定義が重要な意味を持つ.結論からいえば,直観主義論理の含意演算は,
)の定義が重要な意味を持つ.結論からいえば,直観主義論理の含意演算は,
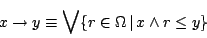 |
(4.14) |
と定義される.この定義は,
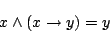 |
(4.15) |
つまり,「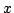 であり,かつ(
であり,かつ(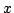 ならば
ならば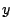 )である」ことが「
)である」ことが「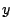 である」ことと一致してほしい(つまりmodus ponesが成立してほしい)という要請に基づくものと解釈することができる.この要請に沿えば,任意の
である」ことと一致してほしい(つまりmodus ponesが成立してほしい)という要請に基づくものと解釈することができる.この要請に沿えば,任意の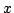 と
と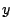 が与えられたときには,
が与えられたときには,
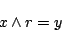 |
(4.16) |
を満たすような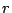 をx
をx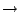 yの真理値とすればよいことになる.しかし,式(4.16)を満たすような
yの真理値とすればよいことになる.しかし,式(4.16)を満たすような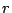 が必ずしも真理値集合
が必ずしも真理値集合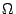 の要素として存在するとは限らない.そこで,式(4.16)の代わりに,
の要素として存在するとは限らない.そこで,式(4.16)の代わりに,
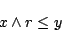 |
(4.17) |
を満たす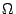 の要素
の要素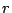 をすべて探し出して,その内で最も
をすべて探し出して,その内で最も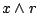 を
を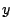 に近づけるもの即ち
に近づけるもの即ち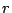 の上限を
の上限を
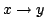 の真理値として採用する.これが式(4.14)の解釈である.
ここで,このように定義した
の真理値として採用する.これが式(4.14)の解釈である.
ここで,このように定義した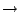 と
と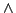 の間には随伴性という非常に重要な性質がある.一般に
の間には随伴性という非常に重要な性質がある.一般に
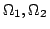 がそれぞれ束で,
がそれぞれ束で,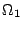 から
から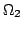 への関数
への関数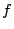 と
と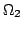 から
から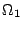 への関数
への関数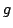 が与えられているとするとき,すべての
が与えられているとするとき,すべての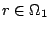 とすべての
とすべての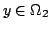 に対して,
に対して,
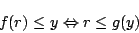 |
(4.18) |
が成立するとき,「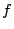 が
が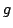 の左随伴である」または「
の左随伴である」または「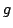 が
が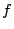 の右随伴である」という.図で表すと図4.6のような関係であり,図4.7がその具体例である.ところで,
の右随伴である」という.図で表すと図4.6のような関係であり,図4.7がその具体例である.ところで,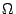 をcHaとし,
をcHaとし,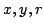 を任意の
を任意の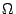 の要素とすると,
の要素とすると,
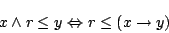 |
(4.19) |
が成立することは,式(4.14)の含意の定義より導かれる.ここで,
| |
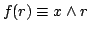 |
|
(4.20) |
| |
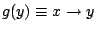 |
|
(4.21) |
と関数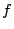 と関数
と関数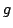 を定義すれば,式(4.19)は式(4.18)となる.これはつまり,「関数
を定義すれば,式(4.19)は式(4.18)となる.これはつまり,「関数
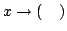 は,関数
は,関数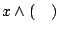 」の左随伴であることを示している(図4.8参照).
」の左随伴であることを示している(図4.8参照).
図 4.6
随伴性の概念図
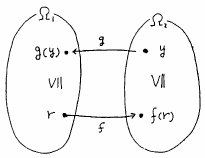 |
図 4.7
随伴関数の例
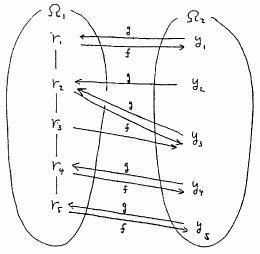 |
図 4.8
含意と連言の随伴性
|
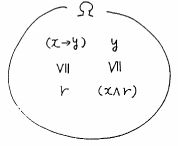
|
直観主義における,真理値集合の構造モデルとして,cHaを仮定するのは,式(4.19)のような随伴性を満たす含意( )が定義できる(必ずしも式(4.14)の定義とは限らない)ことを保証するためである.事実,「
)が定義できる(必ずしも式(4.14)の定義とは限らない)ことを保証するためである.事実,「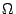 がcHaであること(即ち,完備束
がcHaであること(即ち,完備束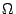 で式(4.13)が成立すること)」と,「完備束
で式(4.13)が成立すること)」と,「完備束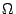 において式(4.19)の随伴性が成り立つ
において式(4.19)の随伴性が成り立つ を定義できること」とは全く同じであることは証明できることがわかっている.
このように,直観主義論理においては,
を定義できること」とは全く同じであることは証明できることがわかっている.
このように,直観主義論理においては,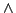 と
と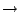 の間に随伴性だけを要請して,cHaを真理値集合として仮定しているため,古典主義のcBaよりも束としてゆるいものを用いていること(公理系としてゆるいものを用いているといってもよい.)ことになる.事実cBaはcHaに含まれており,直観主義論理で成立することはすべて古典論理においても成立する.しかしその逆は成り立たない.
直観主義ではゆるい公理系を用いるため,古典論理の式(4.10)のように,
の間に随伴性だけを要請して,cHaを真理値集合として仮定しているため,古典主義のcBaよりも束としてゆるいものを用いていること(公理系としてゆるいものを用いているといってもよい.)ことになる.事実cBaはcHaに含まれており,直観主義論理で成立することはすべて古典論理においても成立する.しかしその逆は成り立たない.
直観主義ではゆるい公理系を用いるため,古典論理の式(4.10)のように,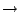 が
が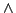 と
と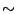 によって表現されてしまうことはなく独立に定義される.また,式(4.9)の排中律を満たす補元が一般に存在しないので,否定は別に定義する必要がある.ここで,式(4.12)の2重否定の性質と式(4.11)のド・モルガン律が成立するような否定
によって表現されてしまうことはなく独立に定義される.また,式(4.9)の排中律を満たす補元が一般に存在しないので,否定は別に定義する必要がある.ここで,式(4.12)の2重否定の性質と式(4.11)のド・モルガン律が成立するような否定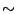 を定義することは可能で,これは古典論的否定あるいは擬否定と呼ばれる.しかし,この擬否定の決め方は一意ではない.つまり,古典論理では,
を定義することは可能で,これは古典論的否定あるいは擬否定と呼ばれる.しかし,この擬否定の決め方は一意ではない.つまり,古典論理では,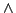 と
と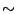 が原始記号であったが,直観主義論理では,
が原始記号であったが,直観主義論理では,
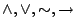 がすべて独立に定義されて原始記号となる.
ここで,擬否定
がすべて独立に定義されて原始記号となる.
ここで,擬否定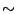 とは別に直観主義論理の含意
とは別に直観主義論理の含意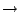 に基づいて,直観主義的な否定
に基づいて,直観主義的な否定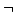 を
を
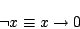 |
(4.22) |
(「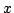 ならば偽」)と定義することができるが,この否定では,式(4.12)のような2重否定の性質を成立せず,3重否定に関して,
ならば偽」)と定義することができるが,この否定では,式(4.12)のような2重否定の性質を成立せず,3重否定に関して,
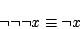 |
(4.23) |
が成立することが知られている.ここで,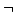 を直観主義的な否定,
を直観主義的な否定, を古典論理的な否定または偽否定と区別して呼ぶこともある.
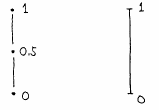
cHaの具体的な例としては,図4.9の3値論理や閉区間
を古典論理的な否定または偽否定と区別して呼ぶこともある.
cHaの具体的な例としては,図4.9の3値論理や閉区間![$[0,1]$](img15.gif) (即ち無限値論理の真理値の集合)などがある.一般に多値論理や無現値論理の場合の真理値集合は,cHaではあるがcBaでは無いので,直観主義論理を用いる必要がある.
(即ち無限値論理の真理値の集合)などがある.一般に多値論理や無現値論理の場合の真理値集合は,cHaではあるがcBaでは無いので,直観主義論理を用いる必要がある.
図 4.9
cHaの例
 |



: 様相論理
: ファジィ論理と種々の論理体系
: 古典論理
目次
平成12年5月17日