


: ファジィ理論と他の論理体系の関係
: ファジィ論理と種々の論理体系
: 直観主義論理
目次
前節にみたように,古典論理の一般化(真理値集合をcBaからcHaへ一般化したという意味での一般化)として直観主義論理が導かれたが,ここで,古典論理の別の方向への一般化とみなされる「様相論理」について説明する.
様相論理で新しく扱う命題は「 であることが必然である」とか「
であることが必然である」とか「 であることが可能である」というような命題である.ここで,様相論理では通常,上の二つの命題を必然を表す論理記号
であることが可能である」というような命題である.ここで,様相論理では通常,上の二つの命題を必然を表す論理記号 と可能を表す論理記号
と可能を表す論理記号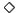 を用いて,
を用いて,
| |
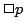 |
|
(4.24) |
| |
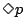 |
|
(4.25) |
と表すことにする.
さて,ここで,式(4.24),式(4.25)の真理値が,どのようになるかが興味のあるところである.そのために古典論理に様相性(ここでは必然性と可能性を指す)に関する公理を追加することになる.ここで,どのような公理を追加するかによって様相論理には多くの体系が存在するが,ここでは,最も標準的な様相論理体系の一つである「体系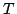 」についてのみ考えるものとする.体系
」についてのみ考えるものとする.体系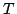 では,古典論理の公理に次の公理が追加される.
では,古典論理の公理に次の公理が追加される.
| |
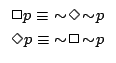 |
 |
(4.26) |
| |
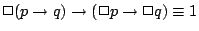 |
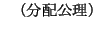 |
(4.27) |
| |
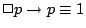 |
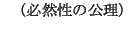 |
(4.28) |
| |
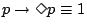 |
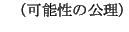 |
(4.29) |
ここで,式(4.26)は公理ではなく定義であるが,内容的には,「 が必然である」ことは「
が必然である」ことは「 でないことが可能でない」ことと同値(あるいは「
でないことが可能でない」ことと同値(あるいは「 が可能である」ことは「
が可能である」ことは「 でないことが必然ではない」ことと同値)であることを表していると了解できる.また式(4.27)は「
でないことが必然ではない」ことと同値)であることを表していると了解できる.また式(4.27)は「 ならば
ならば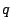 であることが必然的にいえれば,
であることが必然的にいえれば, が必然ならば
が必然ならば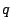 が必然であることは恒に真である」ことを表している.また式(4.28)は「
が必然であることは恒に真である」ことを表している.また式(4.28)は「 が必然ならば
が必然ならば であることは恒に真である」ことを示し,式(4.29)は,「
であることは恒に真である」ことを示し,式(4.29)は,「 ならば
ならば が可能であることは恒に真である」ことを示している.これらは,いずれも内容的に公理と了解してよいように思われる.
ここで例えば,式(4.28)の逆つまり,
が可能であることは恒に真である」ことを示している.これらは,いずれも内容的に公理と了解してよいように思われる.
ここで例えば,式(4.28)の逆つまり,
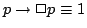 は成立しないだろう.これは,
は成立しないだろう.これは, であるからといって,
であるからといって, が必然とはいえないことからわかる.つまり
が必然とはいえないことからわかる.つまり が成立したとしても,これは,たまたま偶然に成立したのかもしれないから,必ず(必然的に)
が成立したとしても,これは,たまたま偶然に成立したのかもしれないから,必ず(必然的に) だという証拠にはならない.これに対して式(4.29)の可能性の公理
だという証拠にはならない.これに対して式(4.29)の可能性の公理
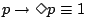 は成立する.これはたとえ偶然であっても
は成立する.これはたとえ偶然であっても が成立すれば
が成立すれば が成立する可能性があることの証拠になることからわかる.
以上のように,様相性を含んだ命題の内容を吟味すると,
が成立する可能性があることの証拠になることからわかる.
以上のように,様相性を含んだ命題の内容を吟味すると,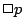 や
や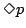 の真理値は
の真理値は の真理値の関数として表せない(
の真理値の関数として表せない( や
や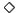 が真理関数的でない)ことにすぐ気がつく.つまり,
が真理関数的でない)ことにすぐ気がつく.つまり, の真理値がわかっても,これからだけでは
の真理値がわかっても,これからだけでは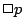 や
や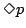 真理値を求めることはできない.たとえ
真理値を求めることはできない.たとえ が真(つまり
が真(つまり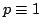 )であっても,それは偶然に真なのか必然的に真なのかは区別がつかないからである.このような様相命題を見通しよく取り扱うモデルとしてKripkeのモデルが有用なので,以下に,これを概観する.
可能性世界意味論では,命題
)であっても,それは偶然に真なのか必然的に真なのかは区別がつかないからである.このような様相命題を見通しよく取り扱うモデルとしてKripkeのモデルが有用なので,以下に,これを概観する.
可能性世界意味論では,命題 は恒にある一定の真理値を持っているのではなく,図4.10のように各々の可能性世界
は恒にある一定の真理値を持っているのではなく,図4.10のように各々の可能性世界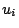 において異なった真理値をもつという立場に立つ.したがって,ある命題の真理値を得るには,命題を指定するだけではなく,可能性世界も指定しなくてはならない.ある一つの命題
において異なった真理値をもつという立場に立つ.したがって,ある命題の真理値を得るには,命題を指定するだけではなく,可能性世界も指定しなくてはならない.ある一つの命題 とある一つの可能性世界
とある一つの可能性世界 を指定したときに,その命題の真理値を与えるものを付値
を指定したときに,その命題の真理値を与えるものを付値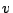 といい,次のように表す.
といい,次のように表す.
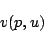 |
(4.30) |
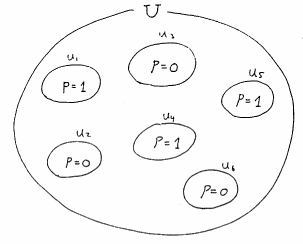
図 4.10
可能性世界の集合と命題の真理値の例
|
|
例えば,図4.10の例の場合は
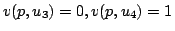 である.また
である.また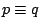 つまり
つまり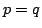 が恒真であることは,すべての
が恒真であることは,すべての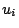 (
(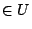 ,
,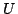 は可能性世界の全体集合)に対して
は可能性世界の全体集合)に対して
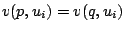 が成立すること,即ち,
が成立すること,即ち,
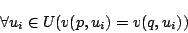 |
(4.31) |
が成立することである.
したがって, が,たまたま世界
が,たまたま世界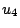 で真(1)になっていることは,
で真(1)になっていることは,
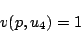 |
(4.32) |
と表されるが,これに対して,恒等式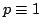 は
は
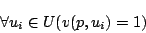 |
(4.33) |
と表される.
ここで,様相命題の真理値について議論するために,上の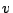 と
と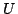 の他に,
の他に,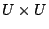 上のある二項関係
上のある二項関係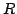 を導入したものがKripkeモデルである.ここで,関係
を導入したものがKripkeモデルである.ここで,関係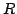 は「ある世界
は「ある世界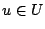 」と「
」と「 から到達可能な世界
から到達可能な世界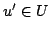 」との関係を定義づける関係であり,
」との関係を定義づける関係であり,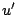 が
が から到達可能であることを
から到達可能であることを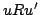 と書き,
と書き, から到達可能な世界すべての集合を
から到達可能な世界すべての集合を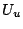 と書くことにする.即ち,
と書くことにする.即ち,
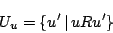 |
(4.34) |
である.
図4.11の例で,
とすれば,例えば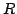 は
は
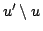 |
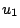 |
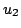 |
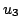 |
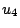 |
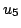 |
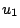 |
1 |
0 |
1 |
0 |
0 |
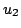 |
0 |
1 |
0 |
0 |
0 |
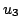 |
0 |
0 |
1 |
0 |
0 |
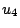 |
0 |
0 |
1 |
1 |
0 |
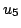 |
0 |
0 |
0 |
0 |
1 |
と定義することができるだろう.ここで,この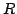 は
は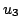 から到達可能な世界は
から到達可能な世界は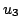 自身と,
自身と,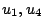 であり,他の世界から到達可能な世界は自分自身だけであることを定義している.またこの場合,
であり,他の世界から到達可能な世界は自分自身だけであることを定義している.またこの場合,
となる.
さてこのように関係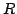 が定義されたとき,
が定義されたとき,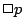 がある世界
がある世界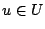 において真(1)であること,つまり,
において真(1)であること,つまり,
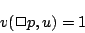 |
(4.35) |
は,
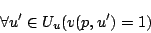 |
(4.36) |
と同値であると定義される.式(4.35)と式(4.36)は「 がある世界
がある世界 において真であることが必然であるということは,
において真であることが必然であるということは, から到達可能なすべての世界
から到達可能なすべての世界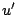 において
において が真となることである」と定義したことを意味する.
また
が真となることである」と定義したことを意味する.
また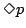 がある世界
がある世界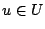 において真(1)であること,つまり,
において真(1)であること,つまり,
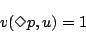 |
(4.37) |
は,
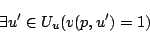 |
(4.38) |
と同値であると定義される.式(4.37)と式(4.38)は「 がある世界
がある世界 において真であることが可能であるということは,
において真であることが可能であるということは, から到達可能なすべての世界
から到達可能なすべての世界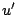 のうちで,
のうちで, が真になる世界が存在することである」と定義したことを意味する.
式(4.35),式(4.36)の定義,および式(4.37),式(4.38)の定義は,さらに,命題
が真になる世界が存在することである」と定義したことを意味する.
式(4.35),式(4.36)の定義,および式(4.37),式(4.38)の定義は,さらに,命題 を真とするすべての集合を
を真とするすべての集合を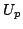 と定義すれば,即ち,
と定義すれば,即ち,
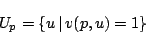 |
(4.39) |
と定義すれば,
|
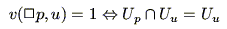
|
(4.40) |
|
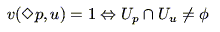
|
(4.41) |
と定義したことと同じであることは容易にわかる.
このように,結局,Kripkeモデルにおいて,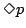 および
および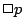 の世界
の世界 での真理値は,
での真理値は, から到達可能な世界すべての集合
から到達可能な世界すべての集合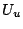 と命題
と命題 が真となる世界すべての集合
が真となる世界すべての集合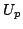 の共通集合を調べることによって式(4.40),式(4.41)のように決定される.
例えば,式(4.11)の例では,
の共通集合を調べることによって式(4.40),式(4.41)のように決定される.
例えば,式(4.11)の例では,
であるから,
となり,
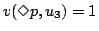 だが,
だが,
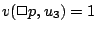 とはならないこと,つまり
とはならないこと,つまり
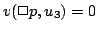 となることがわかる.
このKripkeモデルは
となることがわかる.
このKripkeモデルは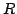 に対する条件を変えることによって様々な様相論理体系を説明できることが知られている.
に対する条件を変えることによって様々な様相論理体系を説明できることが知られている.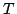 体系の場合は,
体系の場合は,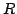 に対する条件として反射律だけを要請する場合,つまりすべての
に対する条件として反射律だけを要請する場合,つまりすべての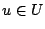 に対して
に対して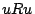 であること(さらにいえばどの世界においても自分自身は必ず到達可能世界であること)だけを要請する場合にあたる.このとき,すべての世界
であること(さらにいえばどの世界においても自分自身は必ず到達可能世界であること)だけを要請する場合にあたる.このとき,すべての世界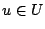 において,式(4.26)から式(4.29)までが成立し,これらが恒真となる.
様相論理では,
において,式(4.26)から式(4.29)までが成立し,これらが恒真となる.
様相論理では, は必然性を,
は必然性を,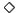 は可能性を表すと解釈するのが通常であるが,そう解釈しなくてはならない必然性はない.必然性と可能性の他にも様相性を表す概念がある.例えば,「義務」と「許容」である.「
は可能性を表すと解釈するのが通常であるが,そう解釈しなくてはならない必然性はない.必然性と可能性の他にも様相性を表す概念がある.例えば,「義務」と「許容」である.「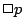 」を「
」を「 とすることは義務である」,「
とすることは義務である」,「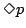 」を「
」を「 とすることは許容される」,「
とすることは許容される」,「 」を「
」を「 をする」と読めば,「
をする」と読めば,「
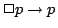 」は「
」は「 をすることが義務ならば
をすることが義務ならば をする」,「
をする」,「
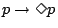 」は「
」は「 をするならば
をするならば は許容されている」,「
は許容されている」,「
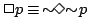 」は「
」は「 をすることが義務であるということは,
をすることが義務であるということは, をしないことが許容されていないことと同じである」と解釈されるのがわかる.
をしないことが許容されていないことと同じである」と解釈されるのがわかる.



: ファジィ理論と他の論理体系の関係
: ファジィ論理と種々の論理体系
: 直観主義論理
目次
平成12年5月17日
![]() は
は![]() から到達可能な世界は
から到達可能な世界は![]() 自身と,
自身と,![]() であり,他の世界から到達可能な世界は自分自身だけであることを定義している.またこの場合,
であり,他の世界から到達可能な世界は自分自身だけであることを定義している.またこの場合,