
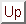


: 様相論理のKripkeモデルと可能性測度,必然性測度
: 可能性,必然性と区間真理値
: クリスプ集合に対する可能性測度と必然性測度
目次
さて前節でみたように,クリスプ集合のみを扱う場合には,式(5.3),式(5.4)によって可能性,必然性が求められた.しかし,ここで扱う集合をファジィ集合に一般化すると,これらの定義で可能性,必然性を求めることは自然ではない.式(5.3),式(5.4)では,共通部分が「ある」か「ない」かによって,可能性,必然性をあるかないか即ち0か1かの2値で評価した.しかし,ファジィ集合の場合は,共通部分があるかないかは2値で判断するべきではなく,「どの程度あるといえるのか」あるいは「どの程度無いといえるのか」を問題としなくてはならない.またその結果,可能性,必然性もあるかないかではなく,それらがどの程度あるのかという程度問題として評価されなくてはならない.
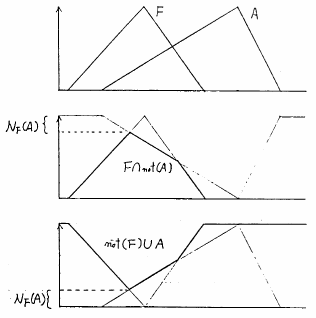
図 5.3
ファジィ集合の可能性測度
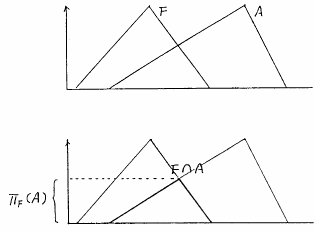 |
図 5.4
極端なファジィ集合の例
 |
まず可能性について考える.前節と同じように,
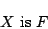 |
(5.5) |
とわかっているときに,
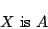 |
(5.6) |
である可能性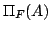 を考える.ただし,今度の場合は,
を考える.ただし,今度の場合は, および
および が共に,ファジィ集合であるものとする.すると,「
が共に,ファジィ集合であるものとする.すると,「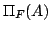 がある」ということは「
がある」ということは「 であってかつ
であってかつ であるような
であるような と
と の共通部分
の共通部分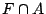 がある」ことだということは前節同様,意味的な問題は無いように思われる.しかしここで
がある」ことだということは前節同様,意味的な問題は無いように思われる.しかしここで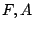 がファジィ集合であることから,一般に
がファジィ集合であることから,一般に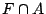 もファジィ集合である.例えば図5.3の場合を考えると
もファジィ集合である.例えば図5.3の場合を考えると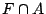 は正規でないファジィ集合となる.ここで,共通部分
は正規でないファジィ集合となる.ここで,共通部分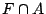 があるということはもう少し正確にいえば,
があるということはもう少し正確にいえば,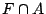 が要素を持つということであるがファジィ集合が要素を持つとはどういうことだろうか.
クリスプ集合の場合は
が要素を持つということであるがファジィ集合が要素を持つとはどういうことだろうか.
クリスプ集合の場合は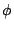 でなければ要素を持つということだし,
でなければ要素を持つということだし,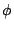 ならば要素を持たないということと考えられる.しかし,ファジィ集合の場合はどうだろうか.例えば,極端な場合,即ち図5.4の
ならば要素を持たないということと考えられる.しかし,ファジィ集合の場合はどうだろうか.例えば,極端な場合,即ち図5.4の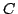 のようなファジィ集合を考えたとき,
のようなファジィ集合を考えたとき,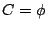 であるが,
であるが,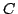 は要素を持つとはほとんどいえないと思われる.これに対して,図5.4の
は要素を持つとはほとんどいえないと思われる.これに対して,図5.4の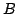 の場合は要素を1つしか持たないが,これははっきり要素を持つといえる.つまり,要素を持つということは,要素をいくつ持つかは関係なく,たとえ一つでもはっきり要素といえるものが存在すればもちろん要素を持つといえるし,いくら多くの要素が0でないグレードをもっていても,それらすべてのグレードが非常に低ければ要素を持つとはいい難くなる.これらから,ファジィ集合が要素を持つといえる度合いは,台集合の要素のどれか一つでよいから最高のグレードを持つものを持ってきて,そのグレードをもって要素を持つ度合いとすればよいことがわかる.つまり,ファジィ集合
の場合は要素を1つしか持たないが,これははっきり要素を持つといえる.つまり,要素を持つということは,要素をいくつ持つかは関係なく,たとえ一つでもはっきり要素といえるものが存在すればもちろん要素を持つといえるし,いくら多くの要素が0でないグレードをもっていても,それらすべてのグレードが非常に低ければ要素を持つとはいい難くなる.これらから,ファジィ集合が要素を持つといえる度合いは,台集合の要素のどれか一つでよいから最高のグレードを持つものを持ってきて,そのグレードをもって要素を持つ度合いとすればよいことがわかる.つまり,ファジィ集合 が要素を持つ度合いは
が要素を持つ度合いは
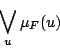 |
(5.7) |
である.図5.4の場合は,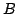 が要素を持つ度合いは1となり,
が要素を持つ度合いは1となり,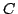 が要素を持つ度合いは0.1となる.
以上のように考えると,
が要素を持つ度合いは0.1となる.
以上のように考えると,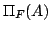 は「
は「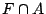 が要素を持つ度合い」と考えてよいだろうから,ファジィ集合の場合,
が要素を持つ度合い」と考えてよいだろうから,ファジィ集合の場合,
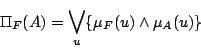 |
(5.8) |
と( のメンバシップ関数が
のメンバシップ関数が
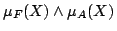 であることに注意して)定義することができ,これが「(
であることに注意して)定義することができ,これが「( is
is  )のとき(
)のとき( is
is  )の可能性」を
)の可能性」を![$[0,1]$](img15.gif) の度合いで示すことになる(図5.3参照).
式(5.5)であるとき式(5.6)である必然性
の度合いで示すことになる(図5.3参照).
式(5.5)であるとき式(5.6)である必然性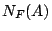 を考える.もちろん
を考える.もちろん および
および が共に,ファジィ集合であるものとする.すると,「
が共に,ファジィ集合であるものとする.すると,「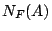 がある」ということは「
がある」ということは「 であってかつ
であってかつ でないような部分つまり,
でないような部分つまり, とnot(
とnot( )の共通部分
)の共通部分
 がない」ことだということは前節と同様,意味的に問題は無いように思われる.ここで,共通部分
がない」ことだということは前節と同様,意味的に問題は無いように思われる.ここで,共通部分
 が無いということはもう少し正確にいえば,
が無いということはもう少し正確にいえば,
 が要素を持たないということである.
可能性測度でみたように,ファジィ集合が要素を持つ度合いは,最高のグレードをもつ要素のグレードであった.同様に考えると,ファジィ集合が要素を持たない度合いは,最も要素らしい要素,即ち最高のグレードを持つ要素が,どの程度,要素ではないといえるかという度合いと考えてよいだろう.これは,即ち要素を持つ度合いの否定である.従って,ファジィ集合
が要素を持たないということである.
可能性測度でみたように,ファジィ集合が要素を持つ度合いは,最高のグレードをもつ要素のグレードであった.同様に考えると,ファジィ集合が要素を持たない度合いは,最も要素らしい要素,即ち最高のグレードを持つ要素が,どの程度,要素ではないといえるかという度合いと考えてよいだろう.これは,即ち要素を持つ度合いの否定である.従って,ファジィ集合 が要素を持たない度合いは,
が要素を持たない度合いは,
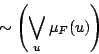 |
(5.9) |
である.
このように考えると,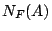 は「
は「
 が要素を持つ度合い」と考えてよいだろうから,ファジィ集合の場合,
が要素を持つ度合い」と考えてよいだろうから,ファジィ集合の場合,
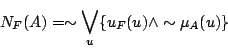 |
(5.10) |
と(
 のメンバシップ関数が
のメンバシップ関数が
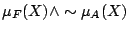 であることに注意して)定義することができ,これが「(
であることに注意して)定義することができ,これが「( is
is  )のとき(
)のとき( is
is  )の必然性」を
)の必然性」を![$[0,1]$](img15.gif) の度合いで示すことになる.ここで,
の度合いで示すことになる.ここで,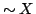 として,
として,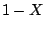 を用いると,式(5.8)は,
を用いると,式(5.8)は,
|
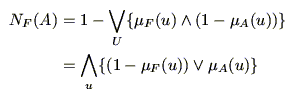
|
(5.11) |
となる.式(5.11)の第1式は
 の最大グレードを1から引いたものであり,第2式は
の最大グレードを1から引いたものであり,第2式は
 の最小グレードであるが,これらが一致することは図5.5より明らかである.
の最小グレードであるが,これらが一致することは図5.5より明らかである.
図 5.5
ファジィ集合の必然性測度
 |
本節で定義した可能性測度(式(5.8)),必然性測度は(式(5.11))をそのままクリスプ集合に適用すれば,前節の式(5.3)および式(5.4)と同じ結果が得られることは容易にわかる.この意味で,式(5.8),式(5.11)は式(5.3),式(5.4)の一般化となっている.しかし,可能性測度,必然性測度の一般化は,本節で行った定義にかぎるわけではない.
一般には,下のような測度が可能性測度として定義される.
- 可能性測度
- 集合
 の部分集合を区間
の部分集合を区間![$[0,1]$](img15.gif) の数値に対応づける集合関数
の数値に対応づける集合関数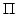 は,次の公理を満たすとき,可能性測度と呼ばれる.
は,次の公理を満たすとき,可能性測度と呼ばれる.
(P1)  かつ
かつ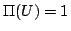
(P2)
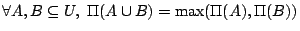
P1は 集合の要素になることは可能でないことと,全体集合の要素となることは可能であることを表している.また,P2は,
集合の要素になることは可能でないことと,全体集合の要素となることは可能であることを表している.また,P2は, の要素かまたは
の要素かまたは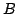 の要素になることが可能な程度は,
の要素になることが可能な程度は, の要素になることが可能な程度と
の要素になることが可能な程度と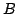 の要素になることが可能な程度のどちらか大きいほうに一致することを表している.これは,可能性の物理的な概念と矛盾していない.もちろん,本節で定義した式(5.8)の測度
の要素になることが可能な程度のどちらか大きいほうに一致することを表している.これは,可能性の物理的な概念と矛盾していない.もちろん,本節で定義した式(5.8)の測度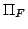 は上の定義を満たしており,可能性測度の一種である.
一方,必然性測度は一般に以下のように定義される.
は上の定義を満たしており,可能性測度の一種である.
一方,必然性測度は一般に以下のように定義される.
- 必然性測度
- 集合
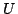 の部分集合を区間
の部分集合を区間![$[0,1]$](img15.gif) の数値に対応づける集合関数
の数値に対応づける集合関数 は次の公理を満たすとき,必然性測度と呼ばれる.
は次の公理を満たすとき,必然性測度と呼ばれる.
(N1) 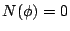 かつ
かつ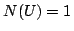
(N2)
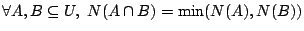
N1は必然的には空集合の要素にならないこと,必然的に全体集合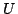 の要素となることを表している.またN2は,必然的に
の要素となることを表している.またN2は,必然的に の要素でもありかつ
の要素でもありかつ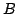 の要素でもあるといえる程度のどちらか小さいほうに一致することを表している.これは必然性の物理的な概念と矛盾していない.式(5.11)の測度
の要素でもあるといえる程度のどちらか小さいほうに一致することを表している.これは必然性の物理的な概念と矛盾していない.式(5.11)の測度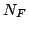 は上の定義を満足しており必然性測度の一種と認められる.
可能性測度,必然性測度は独立に別々のものを定義することも可能であるが,片方を定義して,それから,それと双対な測度を求めることによってもう片方を定義することができる.つまり,P1, P2を満足するある可能性測度
は上の定義を満足しており必然性測度の一種と認められる.
可能性測度,必然性測度は独立に別々のものを定義することも可能であるが,片方を定義して,それから,それと双対な測度を求めることによってもう片方を定義することができる.つまり,P1, P2を満足するある可能性測度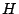 を定義して,それから
を定義して,それから を
を
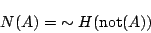 |
(5.12) |
と定義すれば, はN1, N2を自動的に満足することが確かめられる.また逆に
はN1, N2を自動的に満足することが確かめられる.また逆に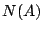 から
から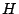 を
を
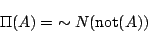 |
(5.13) |
と定義することも可能である.これらは,4.1節の様相論理で述べた可能性,必然性の相互定義可能性(式(4.26))と対応している.
式(5.8)と式(5.11)は別々に定義したが,式(5.12)を満たしており,これらは相互定義可能である.即ち,
|
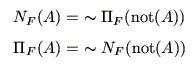
|
(5.14) |
となっている.



: 様相論理のKripkeモデルと可能性測度,必然性測度
: 可能性,必然性と区間真理値
: クリスプ集合に対する可能性測度と必然性測度
目次
平成12年5月17日
