


: ファジィ数の大小の比較
: 可能性,必然性と区間真理値
: 様相論理のKripkeモデルと可能性測度,必然性測度
目次
本節では,タイプ2ファジィ集合の真理値である言語的真理値と可能性,必然性の関係および,それらと,言語的真理値の特別な場合であるところの区間真理値の関係について考察する.
前節では「 is
is  」であるとき「
」であるとき「 is
is  」なる可能性と必然性を求める方法について説明した.一方,第1章では,「
」なる可能性と必然性を求める方法について説明した.一方,第1章では,「 is
is  」であるときに「
」であるときに「 is
is  」なる命題の言語的真理値を求める方法(逆真理値限定)について説明した.ではこの可能性,必然性と言語的真理値にはどんな関係があるだろうか.
ここで,図5.7のような具体的なファジィ集合の例
」なる命題の言語的真理値を求める方法(逆真理値限定)について説明した.ではこの可能性,必然性と言語的真理値にはどんな関係があるだろうか.
ここで,図5.7のような具体的なファジィ集合の例 および
および を考える.このとき,第1章で述べた逆真理値限定法を用いれば,「
を考える.このとき,第1章で述べた逆真理値限定法を用いれば,「 is
is  」であるとき,「
」であるとき,「 is
is  」の言語的真理値
」の言語的真理値 は,
は,
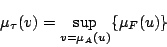 |
(5.21) |
と求められ,図5.7の左側に示すようなメンバシップ関数が得られる.
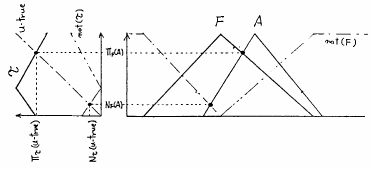
図 5.7
言語的真理値と可能性,必然性の関係
 |
一方,5.2節の議論によれば,式(5.8)および式(5.11)より,「 is
is  」であるときの,「
」であるときの,「 is
is  」の可能性
」の可能性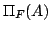 および必然性
および必然性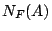 も
も
|
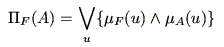
|
(5.22) |
|
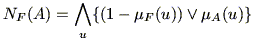
|
(5.23) |
と求められ,図5.7中に示すような結果が得られる.
ここで,図5.7の左側の図において,求められた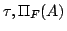 および
および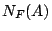 の関係に着目する.すると,
の関係に着目する.すると,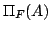 のところで
のところで と
と -trueが交点を持ち,また一方,
-trueが交点を持ち,また一方,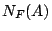 のところで
のところで の否定not(
の否定not( )と
)と -trueが交点を持っているのがわかる.図からみてわかるように,これは即ち,
-trueが交点を持っているのがわかる.図からみてわかるように,これは即ち,
|
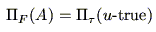
|
(5.24) |
|
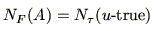
|
(5.25) |
であることを示している.もちろん,
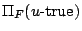 は真理値
は真理値 であるとき,これが
であるとき,これが -trueである可能性であり,また,
-trueである可能性であり,また,
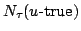 は真理値が
は真理値が であるとき,これが
であるとき,これが -trueである必然性である.即ち,
-trueである必然性である.即ち, -trueのメンバシップ関数が,
-trueのメンバシップ関数が,
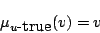 |
(5.26) |
であることに注意すれば,
|
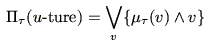
|
(5.27) |
|
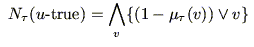
|
(5.28) |
である.
ここで,式(5.21)を式(5.27)に代入すれば,
|
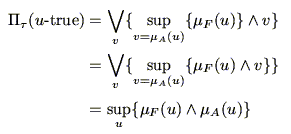
|
(5.29) |
となり,
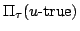 が,式(5.22)の
が,式(5.22)の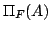 と一致することが確かめられる.
また,式(5.21)を式(5.28)に代入すれば,
と一致することが確かめられる.
また,式(5.21)を式(5.28)に代入すれば,
|
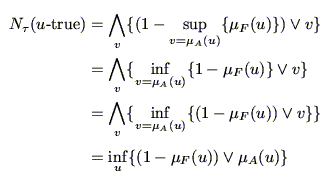
|
(5.30) |
となり,
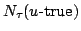 が,式(5.23)の
が,式(5.23)の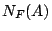 と一致することも確かめられる.
と一致することも確かめられる.
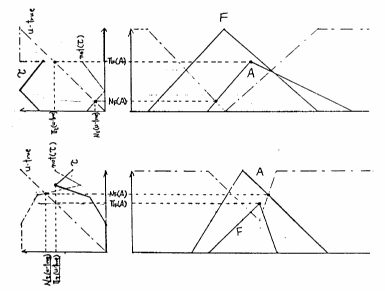
図 5.8
言語的真理値と可能性,必然性の関係(正規でない場合)
|
|
このように,「 is
is  」のとき「
」のとき「 is
is  」である可能性と必然性は,「
」である可能性と必然性は,「 is
is  」のときの「
」のときの「 is
is  」の言語的真理値が
」の言語的真理値が -trueである可能性と必然性に一致することを表してる.
このことは,
-trueである可能性と必然性に一致することを表してる.
このことは, や
や が正規ではない場合にも成立する.例えば,図5.8の上図は
が正規ではない場合にも成立する.例えば,図5.8の上図は が正規でない場合の例,また下図は
が正規でない場合の例,また下図は が正規でない場合の例を示している.それぞれ,このような場合でも,式(5.24)および式(5.25)が成立しているのがわかる.
ところで,図5.8の場合は言語的真理値
が正規でない場合の例を示している.それぞれ,このような場合でも,式(5.24)および式(5.25)が成立しているのがわかる.
ところで,図5.8の場合は言語的真理値 が正規でなくなっている.また可能性と必然性の関係が,
が正規でなくなっている.また可能性と必然性の関係が,
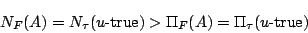 |
(5.31) |
となっており,必然性が可能性より高いという逆転現象が起きている.このような正規でないファジィ真理値や可能性と必然性の逆転現象は「矛盾」の概念と非常に関係が深いと予想される.この矛盾の概念については,まだ,ファジィ理論のなかで十分解明されていない段階であるが,第6章で紹介するファジィ・インターバル論理はこの問題に対する一つのアプローチを与えているので参照されたい.
言語的真理値(ファジィ真理値)の特別な場合として,真理値自体がファジィ集合の特別の集合であるクリスプ集合となっている場合,これを区間真理値という.例えば図5.9に示したものである.区間真理値は![$[0,1]$](img15.gif) 上の区間集合として,
上の区間集合として,![$[n,p]$](img373.gif) と表される.ここで,通常,区間真理値の下限
と表される.ここで,通常,区間真理値の下限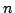 は必然性真理値,また上限
は必然性真理値,また上限 は可能性真理値と呼ばれる.ここで,
は可能性真理値と呼ばれる.ここで,
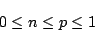 |
(5.32) |
である.
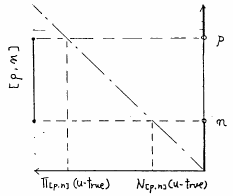
図 5.9
区間真理値の必然性真理値,可能性真理値の解釈
|
|
この区間真理値は,真理値が集合となっているから当然タイプ2ファジィ集合の真理値あるいはグレードとみなされる.ここで,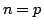 の場合は,区間真理値の特別の場合として
の場合は,区間真理値の特別の場合として![$[0,1]$](img15.gif) 上の数値的真理値,即ち,無限値論理の真理値となる.
区間真理値の特徴は,「無知」の概念を取り扱うことが可能な最も単純な真理値モデルだということであり,実用上の価値は非常に高い.区間真理値の意味するところは,無限値論理のように真理値が確定しておらず,ある範囲内にあることだけがわかっているということである.その区間内のどの真理値にでもなりうるのだが,そのどれなのかはわからないという,いわゆる「部分的無知」の概念を含んでいる.ここで,特別な区間真理値
上の数値的真理値,即ち,無限値論理の真理値となる.
区間真理値の特徴は,「無知」の概念を取り扱うことが可能な最も単純な真理値モデルだということであり,実用上の価値は非常に高い.区間真理値の意味するところは,無限値論理のように真理値が確定しておらず,ある範囲内にあることだけがわかっているということである.その区間内のどの真理値にでもなりうるのだが,そのどれなのかはわからないという,いわゆる「部分的無知」の概念を含んでいる.ここで,特別な区間真理値![$[0,1]$](img15.gif) は真理値のどれなのか全く特定できないことを表すから「完全な無知」を表す.
ここで,
は真理値のどれなのか全く特定できないことを表すから「完全な無知」を表す.
ここで,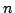 を必然性真理値,
を必然性真理値, を可能性真理値と呼ぶのは,区間真理値
を可能性真理値と呼ぶのは,区間真理値![$[n,p]$](img373.gif) が真理値として,必然的に
が真理値として,必然的に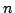 以上は真といえて,
以上は真といえて, まで真ということが可能だということを意味しているからと捉えるのが一般的である.しかし,図5.9に見るように
まで真ということが可能だということを意味しているからと捉えるのが一般的である.しかし,図5.9に見るように
|
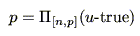
|
(5.33) |
|
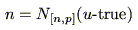
|
(5.34) |
つまり, が「真理値
が「真理値![$[n,p]$](img373.gif) であるときに,その真理値が
であるときに,その真理値が -trueである可能性」,
-trueである可能性」,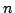 が「真理値が
が「真理値が![$[n,p]$](img373.gif) であるときに,その真理値が
であるときに,その真理値が -trueである必然性」をそれぞれ与えているからであると考えるともっとすっきりする.
いま,図5.10のような言語的真理値
-trueである必然性」をそれぞれ与えているからであると考えるともっとすっきりする.
いま,図5.10のような言語的真理値 が与えられたものとする.ここで,真理値が
が与えられたものとする.ここで,真理値が であるときに,それが
であるときに,それが -trueである可能性と必然性は
-trueである可能性と必然性は
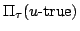 および
および
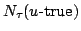 であった.一方,区間真理値
であった.一方,区間真理値![$[n,p]$](img373.gif) を考えると,真理値が
を考えると,真理値が![$[n,p]$](img373.gif) であるときに,それが
であるときに,それが -trueである可能性と必然性は
-trueである可能性と必然性は および
および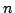 であった.そこで,これらの可能性,必然性が一致するように区間真理値
であった.そこで,これらの可能性,必然性が一致するように区間真理値![$[n,p]$](img373.gif) を決めるとこれは,区間真理値
を決めるとこれは,区間真理値
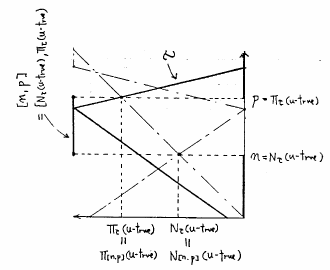
![$[N_\tau(u\mbox{-true}),\Pi_\tau(u\mbox{-true})]$](img377.gif) となる.これを図示すると図5.10のようになり,もとの言語的真理値
となる.これを図示すると図5.10のようになり,もとの言語的真理値 のよい近似を与えているのがわかる.
のよい近似を与えているのがわかる.
図 5.10
区間真理値による言語的真理値の近似
 |
ところで,先に考察したように,「 is
is  」のときの「
」のときの「 is
is  」の言語的真理値を
」の言語的真理値を とすれば,「
とすれば,「 is
is  」のとき,「
」のとき,「 is
is  」である可能性と必然性,即ち,
」である可能性と必然性,即ち,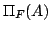 と
と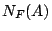 はそれぞれ,
はそれぞれ,
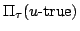 および
および
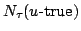 に一致した.ここで,図5.10においてみたように,区間真理値
に一致した.ここで,図5.10においてみたように,区間真理値
![$[N_\tau(u\mbox{-true}),\Pi_\tau(u\mbox{-true})]$](img377.gif) は
は のよい近似になっているから,これは即ち,
のよい近似になっているから,これは即ち,
![$[N_F(A),\Pi_F(A)]$](img379.gif) が
が のよい近似を与えることを意味する.結局,第1章で述べた逆真理値限定によって言語的真理値
のよい近似を与えることを意味する.結局,第1章で述べた逆真理値限定によって言語的真理値 を求めるかわりに,可能性測度,必然性測度により,区間真理値
を求めるかわりに,可能性測度,必然性測度により,区間真理値
![$[N_F(A),\Pi_F(A)]$](img379.gif) を求めると,これは近似的な意味で,「
を求めると,これは近似的な意味で,「 is
is  」を限定する真理値として意味があることがわかる.事実,一般に,可能性測度,必然性測度の計算量は逆真理値限定の計算量にくらべて格段に少ないので,このような近似的な限定真理値を求めることは応用上非常に有効であると思われる.
なお,塚本によって提案された数値的真理値限定は,さらに上の近似を粗くして,
」を限定する真理値として意味があることがわかる.事実,一般に,可能性測度,必然性測度の計算量は逆真理値限定の計算量にくらべて格段に少ないので,このような近似的な限定真理値を求めることは応用上非常に有効であると思われる.
なお,塚本によって提案された数値的真理値限定は,さらに上の近似を粗くして,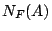 と
と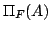 の平均を数値的真理値として求め,これを限定真理値としたことに対応する.
の平均を数値的真理値として求め,これを限定真理値としたことに対応する.



: ファジィ数の大小の比較
: 可能性,必然性と区間真理値
: 様相論理のKripkeモデルと可能性測度,必然性測度
目次
平成12年5月17日