
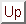


: ファジィ・インターバル論理
: 可能性,必然性と区間真理値
: 言語的真理値と可能性,必然性および区間真理値
目次
DuboisとPradeは可能性と必然性の観点から,ファジィ数の大小比較に関する指標を導入した.ファジィ数の大小の比較は応用面でも重要なので,本節ではこれを概観する.
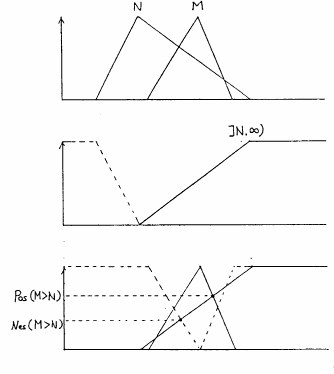
まず,ファジィ数の比較の前に,図5.11の一番上に示す一つのファジィ数 を考え,ここで,
を考え,ここで, 以下の数,
以下の数, 以上の数,
以上の数, より大きい数,
より大きい数, より小さい数がどのようなファジィ数として与えられるかを考える.
より小さい数がどのようなファジィ数として与えられるかを考える.
図 5.11
ファジィ数 に対する大小の概念
に対する大小の概念
 |
 以下の数は,「ファジィ数
以下の数は,「ファジィ数 より可能的に等しいか小さいファジィ数」と考え,
より可能的に等しいか小さいファジィ数」と考え,![$(-\infty ,N]$](img381.gif) と表し,そのメンバシップ関数は
と表し,そのメンバシップ関数は
![\begin{displaymath}
\mu_{(-\infty,N]}(U)=\Pi_N([u,\infty))
\end{displaymath}](img382.gif) |
(5.35) |
と定義される.つまり, が
が 以下の数であるといえる度合いは,
以下の数であるといえる度合いは, が
が であるとしたときに,
であるとしたときに, が
が 自身以上の集合に含まれている可能性に等しいと定義したことになる.これは,もし,
自身以上の集合に含まれている可能性に等しいと定義したことになる.これは,もし, が
が 以下の数ならば,
以下の数ならば, が
が であると仮定したとき,その仮定が,
であると仮定したとき,その仮定が, の可能性分布を実際の
の可能性分布を実際の よりも小さいほうに引き下げることはないから,
よりも小さいほうに引き下げることはないから, が「実際の
が「実際の 自身以上の集合」に含まれる可能性が高くなることに関係している.これを,図で表せば,図5.11の2段目の図となる.
自身以上の集合」に含まれる可能性が高くなることに関係している.これを,図で表せば,図5.11の2段目の図となる.
 より大きい数は,「ファジィ数
より大きい数は,「ファジィ数 より必然的に大きいファジィ数」と考え,
より必然的に大きいファジィ数」と考え,![$]N,\infty)$](img383.gif) と表す.これは,
と表す.これは, 以下の数の否定の概念であるから,式(5.35)の否定をとればよい.これを図で表せば,図5.11の3段目の図となる.
以下の数の否定の概念であるから,式(5.35)の否定をとればよい.これを図で表せば,図5.11の3段目の図となる.
 以上の数は,「ファジィ数
以上の数は,「ファジィ数 より可能的に等しいか大きいファジィ数」と考え,
より可能的に等しいか大きいファジィ数」と考え,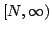 と表し,そのメンバシップ関数は
と表し,そのメンバシップ関数は
![\begin{displaymath}
\mu_{[N,\infty)}(u)=\Pi_N((-\infty,u])
\end{displaymath}](img385.gif) |
(5.36) |
と 以下の数の場合と同様な議論により定義される.これを図に示せば,図5.11の4段目の図が得られる.
以下の数の場合と同様な議論により定義される.これを図に示せば,図5.11の4段目の図が得られる.
 より小さい数は,「ファジィ数
より小さい数は,「ファジィ数 より必然的に小さいファジィ数」と考え,
より必然的に小さいファジィ数」と考え,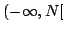 と表す.これは,
と表す.これは, 以上の数の否定の概念であるから,式(5.36)の否定をとればよい.これを図で表せば,図5.11の5段目の図となる.
次に,二つのファジィ数
以上の数の否定の概念であるから,式(5.36)の否定をとればよい.これを図で表せば,図5.11の5段目の図となる.
次に,二つのファジィ数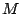 と
と の比較について考える.ここで,図5.12の
の比較について考える.ここで,図5.12の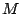 と
と を例にとり,
を例にとり,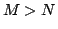 であるかどうかを調べる.このための指標として,
であるかどうかを調べる.このための指標として,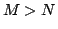 である可能性Pos
である可能性Pos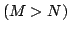 ,必然性Nes
,必然性Nes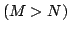 が次のように,定義される.
が次のように,定義される.
|
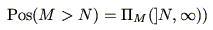
|
(5.37) |
|
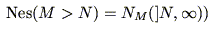
|
(5.38) |
これらは,「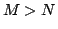 である可能性,必然性」をそれぞれ,「
である可能性,必然性」をそれぞれ,「 であるとき,これが
であるとき,これが より大きい数である可能性,必然性」と定義したことに他ならない.図5.12の例で下段の図のような可能性,必然性が得られる.
より大きい数である可能性,必然性」と定義したことに他ならない.図5.12の例で下段の図のような可能性,必然性が得られる.
図 5.12
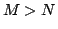 の可能性と必然性
の可能性と必然性
 |
同様にして,
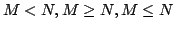 の可能性,必然性も定義されることは容易に想像がつくであろう.
ここで,一般に,
の可能性,必然性も定義されることは容易に想像がつくであろう.
ここで,一般に,
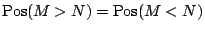 などの関係が成立しないことに注意する必要がある.
などの関係が成立しないことに注意する必要がある.
平成12年5月17日
