
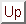


: FI真理値における二つの半順序関係:「真偽」と「曖昧さ」
: ファジィ・インターバル論理
: ファジィ・インターバル論理
目次
ファジィ・インターバル(以後FIと略す)論理における真理値モデル(以後FI真理値と呼ぶ)は区間真理値と同様に,必然性真理値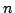 と可能性真理値
と可能性真理値 のペアによって決定され,
のペアによって決定され,![$[n,p]$](img373.gif) と表現される.ただしここで,
と表現される.ただしここで, と
と に関する条件は,
に関する条件は,
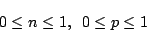 |
(6.1) |
だけであり,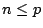 以下である必要はなく,
以下である必要はなく,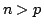 であってもよいところが区間真理値とは違うところである.
ここで,FI真理値
であってもよいところが区間真理値とは違うところである.
ここで,FI真理値![$[n,p]$](img373.gif) のメンバシップ関数は,
のメンバシップ関数は,
|
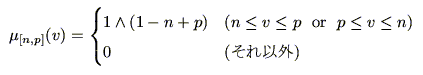
|
(6.2) |
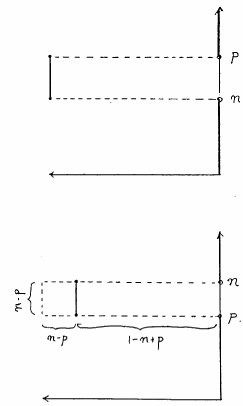
と定義される.このメンバシップ関数の例を示すと図6.1のようになる.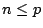 の場合は,結果的に通常の区間真理値と一致する(図6.1の上図)が,一方,
の場合は,結果的に通常の区間真理値と一致する(図6.1の上図)が,一方,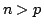 の場合は図6.1の下図に示すように,正規でないファジィ集合となる.つまり,
の場合は図6.1の下図に示すように,正規でないファジィ集合となる.つまり, の場合は,区間真理値
の場合は,区間真理値![$[n,p]$](img373.gif) の高さを
の高さを だけ下げた形になる.
だけ下げた形になる.
図 6.1
FI真理値のメンバシップ関数の例
|
|
図6.1の下図のFI真理値は, から
から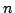 までの間の真理値のどれかをとる可能性は
までの間の真理値のどれかをとる可能性は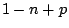 程度あるが,しかしどれ一つとして,完全に(程度1で)真理値となりうるものはないことを示している.これは,真理値としてどれも選択できないことを表しており,「部分的矛盾」を表していると考えられる.またこれは,FIの極端な場合,即ち,
程度あるが,しかしどれ一つとして,完全に(程度1で)真理値となりうるものはないことを示している.これは,真理値としてどれも選択できないことを表しており,「部分的矛盾」を表していると考えられる.またこれは,FIの極端な場合,即ち,![$[1,0]$](img398.gif) を考えるともっとはっきりする.
を考えるともっとはっきりする.![$[1,0]$](img398.gif) のメンバシップ関数は式(6.2)の定義に従えば,すべての真理値でグレードが0となる.これは真理値として,どれも全く選びようがないことを,つまり,真偽を定めることが全く意味がないことを表現している.
このように,式(6.2)で定義されたFI真理値のメンバシップ関数は,
のメンバシップ関数は式(6.2)の定義に従えば,すべての真理値でグレードが0となる.これは真理値として,どれも全く選びようがないことを,つまり,真偽を定めることが全く意味がないことを表現している.
このように,式(6.2)で定義されたFI真理値のメンバシップ関数は,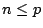 では区間真理値に一致し,
では区間真理値に一致し,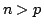 という矛盾を含む局面では,正規でないファジィ真理値を与えるという意味で受け入れることはできる.しかし,なぜ図6.1の定義を行うかという積極的な根拠は論文
という矛盾を含む局面では,正規でないファジィ真理値を与えるという意味で受け入れることはできる.しかし,なぜ図6.1の定義を行うかという積極的な根拠は論文![${}^{[10]}$](img9.gif) でも明らかにされていない.また論文の筆者に,直接問い合わせたところでも,FI真理値のメンバシップ関数の定義を図6.1とする必然性は無いとのことであった.また,区間真理値の
でも明らかにされていない.また論文の筆者に,直接問い合わせたところでも,FI真理値のメンバシップ関数の定義を図6.1とする必然性は無いとのことであった.また,区間真理値の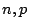 の場合は,式(5.33),式(5.34)のような意味があったが,FI真理値の
の場合は,式(5.33),式(5.34)のような意味があったが,FI真理値の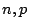 ではそのような意味づけが必ずしもできないという問題もある.したがって式(6.2)のメンバシップ関数の定義については,今後,議論を詰める余地があるように思われる.ただここで,一つ興味深いのはFI真理値の高さが,
ではそのような意味づけが必ずしもできないという問題もある.したがって式(6.2)のメンバシップ関数の定義については,今後,議論を詰める余地があるように思われる.ただここで,一つ興味深いのはFI真理値の高さが,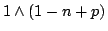 つまり,Lukasiewicz含意によるところの
つまり,Lukasiewicz含意によるところの
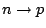 (必然ならば可能)の真理値になっているところである.
(必然ならば可能)の真理値になっているところである.
平成12年5月17日