


: 逆真理値限定
: ファジィ命題の逆真理値限定
: ファジィ命題の逆真理値限定
目次
ここでは,「逆真理値限定」について説明する準備として,前報告書![${}^{[1]}$](img13.gif) で説明した「言語的真理値限定」について概説する.
言語的真理値限定命題とは,「
で説明した「言語的真理値限定」について概説する.
言語的真理値限定命題とは,「 is
is  」というファジィ命題に対して,ある言語的真理値
」というファジィ命題に対して,ある言語的真理値 (
( は真理値空間
は真理値空間![$[0,1]$](img15.gif) を台集合とするファジィ数)による限定を行い,
を台集合とするファジィ数)による限定を行い,
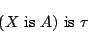 |
(1.1) |
なる新たなファジィ命題をつくったときに,この命題の真理値が に関してどのように変化するかを調べるものであった.換言すれば,これは,式(1.1)のファジィ命題の標準形
に関してどのように変化するかを調べるものであった.換言すれば,これは,式(1.1)のファジィ命題の標準形
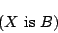 |
(1.2) |
を求めることであり,具体的には,すべての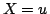 (
(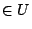 ,
,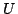 は変数
は変数 の定義域)において式(1.1)と式(1.2)の真理値が一致するようにファジィ集合
の定義域)において式(1.1)と式(1.2)の真理値が一致するようにファジィ集合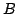 のメンバシップ関数
のメンバシップ関数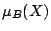 の形を求めることである.
さて,ここで,式(1.1)の言語的真理値限定ファジィ命題は次のように解釈される.ファジィ命題「
の形を求めることである.
さて,ここで,式(1.1)の言語的真理値限定ファジィ命題は次のように解釈される.ファジィ命題「 is
is  」に対して,
」に対して, の値が一つ具体的に与えられれば,「
の値が一つ具体的に与えられれば,「 is
is  」自身は区間
」自身は区間![$[0,1]$](img15.gif) のある実数を真理値として持つ.これはつまり,「
のある実数を真理値として持つ.これはつまり,「 is
is  」自体が区間
」自体が区間![$[0,1]$](img15.gif) を定義域として持つ実数変数に他ならないことを示している(一般に論理学では,命題と真理値は全く同一視されることに注意.).そこで,実数変数
を定義域として持つ実数変数に他ならないことを示している(一般に論理学では,命題と真理値は全く同一視されることに注意.).そこで,実数変数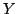 を導入して,
を導入して,
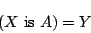 |
(1.3) |
とおけば,式(1.1)は,
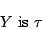 |
(1.4) |
と標準形になっているから,このファジィ命題の真理値は,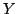 を変数として,
を変数として,
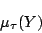 |
(1.5) |
と得られることがわかる.ところで,変数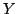 (つまり「
(つまり「 is
is  」の真理値,あるいは「
」の真理値,あるいは「 is
is  」そのものと考えてもよい.)は
」そのものと考えてもよい.)は の値によって
の値によって
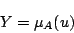 |
(1.6) |
と得られるから,式(1.6)を式(1.5)に代入すれば,
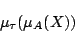 |
(1.7) |
が得られ,これが,式(1.4)のファジィ命題,さらには,式(1.1)のファジィ命題の真理値を与えることになる.ここで,式(1.7)は結果的には の関数となっているから,これを式(1.2)のファジィ集合
の関数となっているから,これを式(1.2)のファジィ集合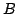 のメンバシップ関数として,
のメンバシップ関数として,
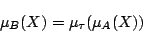 |
(1.8) |
と採用することができ,このとき,式(1.1)と式(1.2)の命題はすべての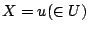 において同じ真理値を持つことになり,同一の命題となる(一般に論理学において,命題とは真理値そのものであり,その中身がどのような形で表現されていようとも,考えているすべての状況下で,真理値が一致しているようなふたつの命題は同一のものとみなされる.).
以上のように,式(1.1)のような形の言語的真理値限定ファジィ命題が与えられたときには,式(1.8)のようなメンバシップ関数をもつファジィ集合
において同じ真理値を持つことになり,同一の命題となる(一般に論理学において,命題とは真理値そのものであり,その中身がどのような形で表現されていようとも,考えているすべての状況下で,真理値が一致しているようなふたつの命題は同一のものとみなされる.).
以上のように,式(1.1)のような形の言語的真理値限定ファジィ命題が与えられたときには,式(1.8)のようなメンバシップ関数をもつファジィ集合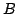 を求めることにより,与えられた命題と全く同一の命題を式(1.2)のような標準形で求めることができ,この過程が「真理値限定」と呼ばれる.
を求めることにより,与えられた命題と全く同一の命題を式(1.2)のような標準形で求めることができ,この過程が「真理値限定」と呼ばれる.
図 1.1
言語的真理値限定の例
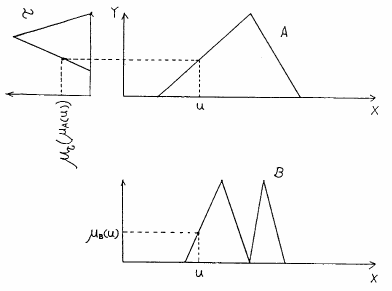 |
例えば.図1.1の上図に示すようなファジィ集合 と言語的真理値
と言語的真理値 のメンバシップ関数により式(1.1)の真理値限定ファジィ命題が与えられているとすれば,式(1.8)により,図1.1の下図のようなファジィ集合
のメンバシップ関数により式(1.1)の真理値限定ファジィ命題が与えられているとすれば,式(1.8)により,図1.1の下図のようなファジィ集合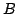 のメンバシップ関数が得られ,このとき,式(1.2)のファジィ標準形命題は,与えられた真理値限定ファジィ命題と同一となる.試みに図のように適当に
のメンバシップ関数が得られ,このとき,式(1.2)のファジィ標準形命題は,与えられた真理値限定ファジィ命題と同一となる.試みに図のように適当に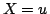 とおいてみても,式(1.1)の真理値
とおいてみても,式(1.1)の真理値
と式(1.2)の命題の真理値
が一致するようになっているのがわかる.



: 逆真理値限定
: ファジィ命題の逆真理値限定
: ファジィ命題の逆真理値限定
目次
平成12年5月17日