


: 逆真理値限定の用途
: ファジィ命題の逆真理値限定
: 真理値限定と真理値限定命題
目次
逆真理値限定は,その名が示す通り,真理値限定の逆の過程である.真理値限定では,式(1.1)の と
と がわかっているときに,
がわかっているときに,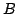 を求める問題であった.これに対して,逆真理値限定とは,式(1.2)の
を求める問題であった.これに対して,逆真理値限定とは,式(1.2)の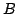 と式(1.1)の
と式(1.1)の がわかっているときに,式(1.2)の命題と式(1.1)の命題が同一の命題となるように,ファジィ真理値
がわかっているときに,式(1.2)の命題と式(1.1)の命題が同一の命題となるように,ファジィ真理値 を(即ち,
を(即ち, のメンバシップ関数を)求める過程である.
ここで,まず簡単な場合,つまり,式(1.1)のメンバシップ関数
のメンバシップ関数を)求める過程である.
ここで,まず簡単な場合,つまり,式(1.1)のメンバシップ関数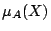 が1対1の写像になっている場合を考える.この場合には,
が1対1の写像になっている場合を考える.この場合には,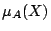 の逆関数
の逆関数
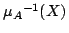 が存在して,
が存在して,
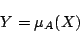 |
(1.9) |
とおけば,
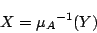 |
(1.10) |
となる.ここで,式(1.1)と式(1.2)の命題が同値となる必要十分条件は式(1.8)が成立することであるから,式(1.9)と式(1.10)を式(1.8)に代入すれば,
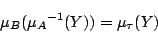 |
(1.11) |
となり,結局 のメンバシップ関数は求められる.
しかし一般には,
のメンバシップ関数は求められる.
しかし一般には, のメンバシップ関数
のメンバシップ関数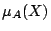 は
は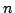 対1の写像であり,逆関数が定まらない.即ち,
対1の写像であり,逆関数が定まらない.即ち,
とおいたとき,これを満たす は
は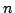 個存在する.したがって,同値の必要十分条件である式(1.8)にこれを代入しても,
個存在する.したがって,同値の必要十分条件である式(1.8)にこれを代入しても,
は一つの値に定まらない.そこでこの場合は,それら上限をとって を定めることにしている.つまり,
を定めることにしている.つまり,
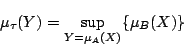 |
(1.12) |
と求められる.
図 1.2
逆真理値限定の例
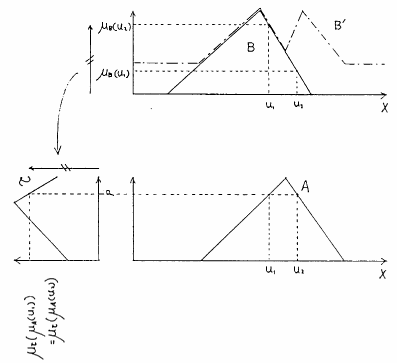 |
図1.2に逆真理値限定の例を示す.ここで,例えば, の
の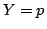 のときのグレード,即ち
のときのグレード,即ち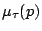 を求めるとする.このとき,
を求めるとする.このとき,
となる は,
は,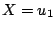 と
と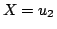 のふたつがあるから,
のふたつがあるから,
となり,結局,
が得られる.
以上のように,式(1.12)に従えば, が
が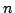 対1のメンバシップ関数を持つ場合にも,式(1.1)の限定真理値
対1のメンバシップ関数を持つ場合にも,式(1.1)の限定真理値 のメンバシップ関数を求めることが一応可能となる.しかし,ここで求められた真理値限定命題(式(1.8))が成立しているわけでなく,
のメンバシップ関数を求めることが一応可能となる.しかし,ここで求められた真理値限定命題(式(1.8))が成立しているわけでなく,
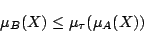 |
(1.13) |
が成立しているにすぎないことから直ちにわかる.試みに,図1.2の場合,式(1.12)で を求めて,式(1.1)の形の真理値限定命題をつくり,これに対してさらに,真理値限定を行って,標準形命題に戻してやると,図1.2中の
を求めて,式(1.1)の形の真理値限定命題をつくり,これに対してさらに,真理値限定を行って,標準形命題に戻してやると,図1.2中の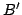 (一点鎖線で示す二山のメンバシップ関数)が得られて,
(一点鎖線で示す二山のメンバシップ関数)が得られて,
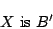 |
(1.14) |
が得られてしまう.これが,もともとの命題
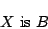 |
(1.15) |
と同値でないのは明らかである.ただし,式(1.13)から,
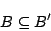 |
(1.16) |
が成立しているから,継承原理に従えば,式(1.15)と式(1.16)から式(1.14)が推論されることはいえる.
このように,一般に逆真理値限定によって得られる.真理値限定命題は,もとの命題とは同値にはならず,もとの命題から継承原理によって推論されかつ真理値限定命題で表されうる命題のうちでもっとも小さいものを求めていることになる.



: 逆真理値限定の用途
: ファジィ命題の逆真理値限定
: 真理値限定と真理値限定命題
目次
平成12年5月17日