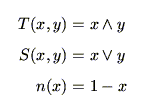


: ファジィ推論の数学的解釈
: ファジィ理論の数学的基礎
: 三角型ファジィ数とその計算
目次
前節までで議論してきたファジィ集合は,メンバシップ関数によって曖昧な集合を取り扱ってきたが,そのメンバシップ関数自体,即ち,各グレードはある確定値で定義されてきた.これはつまり,ある要素に対するグレード区間![$[0,1]$](img106.gif) のある実数としてクリスプにしかもただ1点として与えられたこと他ならない.
そこで,これを拡張し,グレード自体を,区間
のある実数としてクリスプにしかもただ1点として与えられたこと他ならない.
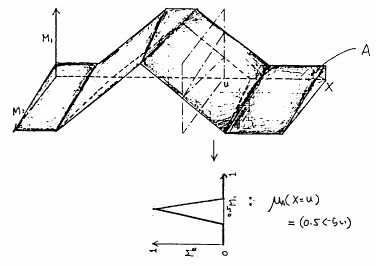
そこで,これを拡張し,グレード自体を,区間![$[0,1]$](img106.gif) 上のファジィ数として定義したものがタイプ2ファジィ集合と呼ばれるファジィ集合である(タイプ2ファジィ集合との対比をすれば,通常のファジィ集合はタイプ1ファジィ集合と呼ばれる.).タイプ2ファジィ集合の例をスケッチすれば,例えば,図4.30のようになるだろう.図で,例えば,
上のファジィ数として定義したものがタイプ2ファジィ集合と呼ばれるファジィ集合である(タイプ2ファジィ集合との対比をすれば,通常のファジィ集合はタイプ1ファジィ集合と呼ばれる.).タイプ2ファジィ集合の例をスケッチすれば,例えば,図4.30のようになるだろう.図で,例えば,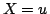 のときのグレードをみると,グレードは,「だいたい0.5位」というファジィ数(ファジィ集合)
のときのグレードをみると,グレードは,「だいたい0.5位」というファジィ数(ファジィ集合)
![$\subseteq [0,1]$](img313.gif) となっている.
となっている.
図 4.30
タイプ2ファジィ集合の例
 |
次に,タイプ2ファジィ集合間の演算は,通常のファジィ集合間の演算の拡張として,容易に類推される.つまり,通常のファジィ集合では,同じ要素上のグレード間に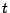 - ノルム
- ノルム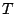 ,
,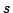 - ノルム
- ノルム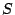 や否定演算not()を作用させたが,ここでは,グレード自体がファジィ集合なので,上の演算をファジィ数間の演算として拡張原理を用いて行うことになる.
例えば,
や否定演算not()を作用させたが,ここでは,グレード自体がファジィ集合なので,上の演算をファジィ数間の演算として拡張原理を用いて行うことになる.
例えば,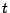 - ノルムとして論理積(
- ノルムとして論理積(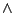 )を用いる場合,ファジィ・グレード(ファジィ数により表されたグレード)
)を用いる場合,ファジィ・グレード(ファジィ数により表されたグレード)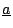 と
と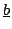 の間の演算,
の間の演算,
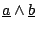 は,ファジィ数間の演算として,拡張原理により,図4.31のように求まる(ここで,図示の具合上,ファジィ数のメンバシップ関数を横置きにして図示しているのに注意).図の例では,
は,ファジィ数間の演算として,拡張原理により,図4.31のように求まる(ここで,図示の具合上,ファジィ数のメンバシップ関数を横置きにして図示しているのに注意).図の例では,
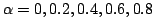 の場合についてみているが,実際に
の場合についてみているが,実際に を
を![$(0,1]$](img232.gif) とした場合には,連続なファジィ数として,
とした場合には,連続なファジィ数として,
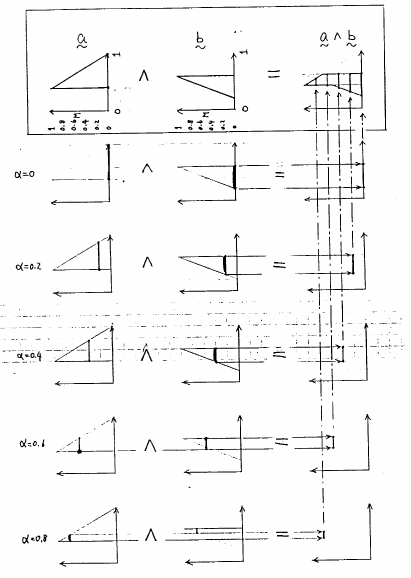
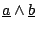 が求まることが推察されるだろう.図4.32には,もっともよく使われる,
が求まることが推察されるだろう.図4.32には,もっともよく使われる,
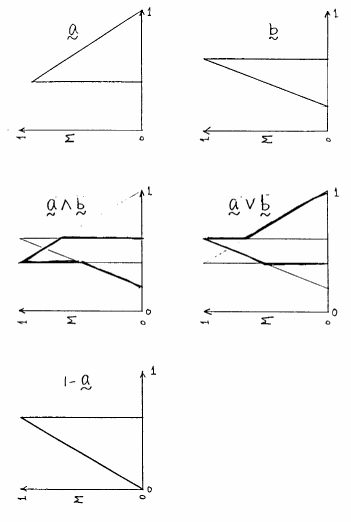
の各演算をファジィ数に施した結果の例を示す.
図 4.31
ファジィ・グレード間の区間分析法による演算例:論理積の場合
|
|
図 4.32
ファジィ・グレード間の演算結果例
 |
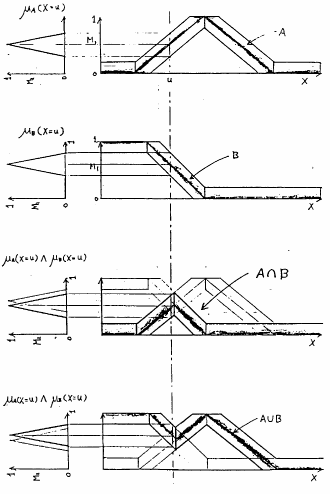
このようなファジィ数間の演算を各ファジィ・グレード間に施せば,タイプ2ファジィ集合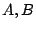 間の基本演算は結果的に図4.33のように得られる.例えば,
間の基本演算は結果的に図4.33のように得られる.例えば,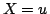 におけるタイプ2ファジィ集合
におけるタイプ2ファジィ集合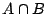 のメンバシップ関数の値,即ちグレードは,
のメンバシップ関数の値,即ちグレードは,
であるが,これは,図中では,三角型のファジィ数として得られているのがわかる.
図 4.33
タイプ2ファジィ集合間の基本演算例
 |
タイプ2ファジィ集合のメンバシップ関数のグレードのメンバシップ関数のグレードをさらにファジィ化するとタイプ3ファジィ集合が定義される.このように一般にタイプ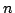 ファジィ集合が定義される.しかし,実用上は,タイプ2ファジィ集合までが用いられる.
タイプ2ファジィ集合の発見は,ファジィ理論において非常に大きな役割をはたしている.タイプ2ファジィ集合の最大の応用として,推論における言語的真理値を表すために用いられているが,これによって,「だいたい真」,「真でも偽でもない」,「真理がわからない」などの真理値を取り扱うことができるようになり,推論技術が飛躍的に進歩した.これに対して,タイプ1ファジィ集合しか用いない推論は,多値論理あるいはその延長としての無限値論理と(ファジィ理論における数学的取り扱いの統一性のよさを別にすれば)扱える真理値には本質において違いがないといえる.この言語的真理値を用いた推論については,5.5で述べる.
ファジィ集合が定義される.しかし,実用上は,タイプ2ファジィ集合までが用いられる.
タイプ2ファジィ集合の発見は,ファジィ理論において非常に大きな役割をはたしている.タイプ2ファジィ集合の最大の応用として,推論における言語的真理値を表すために用いられているが,これによって,「だいたい真」,「真でも偽でもない」,「真理がわからない」などの真理値を取り扱うことができるようになり,推論技術が飛躍的に進歩した.これに対して,タイプ1ファジィ集合しか用いない推論は,多値論理あるいはその延長としての無限値論理と(ファジィ理論における数学的取り扱いの統一性のよさを別にすれば)扱える真理値には本質において違いがないといえる.この言語的真理値を用いた推論については,5.5で述べる.
平成12年5月17日