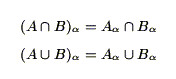


: 拡張原理
: ファジィ理論の数学的基礎
: ファジィ関係の演算
目次
前節までで,任意のファジィ集合 は台集合(全体集合)上に定義されたメンバシップ関数という形で表すことができ,台集合のある要素
は台集合(全体集合)上に定義されたメンバシップ関数という形で表すことができ,台集合のある要素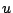 に対するメンバシップ関数の高さ
に対するメンバシップ関数の高さ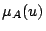 が,その要素の
が,その要素の に対するグレードを表すというようにとらえてきた.いわばメンバシップ関数を縦割りで見てきた.ここでは,このメンバシップ関数を横割りで見るための道具だてとして用いられる「
に対するグレードを表すというようにとらえてきた.いわばメンバシップ関数を縦割りで見てきた.ここでは,このメンバシップ関数を横割りで見るための道具だてとして用いられる「 レベル集合」という概念について説明する.(注意:「
レベル集合」という概念について説明する.(注意:「 レベル集合」は,「
レベル集合」は,「 カット」と呼ばれる概念の一種である.
カット」と呼ばれる概念の一種である. カットには「弱
カットには「弱 カット」と「強
カット」と「強 カット」の二種類があるが,このうち特に「弱
カット」の二種類があるが,このうち特に「弱 カット」のことを「
カット」のことを「 レベル集合」と呼ぶ.)
台集合(全体集合)
レベル集合」と呼ぶ.)
台集合(全体集合)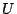 におけるファジィ集合
におけるファジィ集合 と任意の実数
と任意の実数
![$\alpha\,(\alpha\in (0,1]$](img229.gif) ,つまり
,つまり
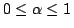 )に対して,
)に対して, におけるグレードが
におけるグレードが 以上であるような
以上であるような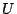 の要素の集合を
の要素の集合を レベル集合といい,
レベル集合といい,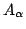 で表す.即ち,
で表す.即ち,
である.
ここで, レベル集合
レベル集合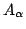 は,クリスプ集合であることと,区間
は,クリスプ集合であることと,区間![$(0,1]$](img232.gif) の中のすべての実数
の中のすべての実数 について定義されることに注意する.
例えば,図4.20はファジィ集合
について定義されることに注意する.
例えば,図4.20はファジィ集合 に対する,
に対する,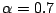 の場合の
の場合の レベル集合
レベル集合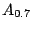 のメンバシップ関数を示している.この例の場合は,メンバシップ関数のグレードが0.7以上になる
のメンバシップ関数を示している.この例の場合は,メンバシップ関数のグレードが0.7以上になる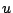 の集合である.
上で定義された
の集合である.
上で定義された レベル集合を組み合わせると逆に元のファジィ集合が再構成される.これが,以下の「分解定理」と呼ばれるものである.
ファジィ集合
レベル集合を組み合わせると逆に元のファジィ集合が再構成される.これが,以下の「分解定理」と呼ばれるものである.
ファジィ集合 はその
はその レベル集合により次のように分解できる.
レベル集合により次のように分解できる.
ここで,
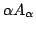 はクリスプ集合
はクリスプ集合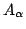 のメンバシップ関数の高さをすべて,
のメンバシップ関数の高さをすべて, 倍したものであり,
倍したものであり,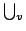 は論理和(
は論理和(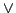 )で定義された場合の結び(
)で定義された場合の結び(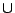 )を特に意味するものとする.
14pt
)を特に意味するものとする.
14pt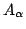 はクリスプ集合だが,
はクリスプ集合だが,
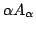 は一般にもはやクリスプ集合ではないことに注意.例えば
は一般にもはやクリスプ集合ではないことに注意.例えば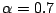 の場合の
の場合の
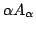 即ち
即ち
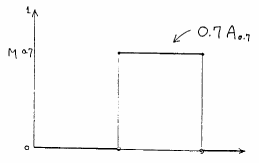
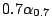 は図4.21のようになる.このメンバシップ関数は矩形だが0.7という
は図4.21のようになる.このメンバシップ関数は矩形だが0.7という 以外のグレードを持つからファジィ集合である.
以外のグレードを持つからファジィ集合である.
図 4.21
ファジィ集合
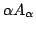
 |
上のようにファジィ集合 は無限個の
は無限個の
![$\alpha\,(\in(0,1])$](img239.gif) に対応する無限個の
に対応する無限個の
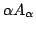 の結びで表されるが,このとき,結び
の結びで表されるが,このとき,結び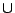 として,論理和(
として,論理和(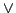 )で定義されたもの(本報告ではこの意味での
)で定義されたもの(本報告ではこの意味での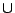 を特に区別して,
を特に区別して,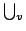 とかくことにする.)を用いなければ,上の分解定理は成立しないと思われる.一般の文献では単に
とかくことにする.)を用いなければ,上の分解定理は成立しないと思われる.一般の文献では単に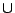 を使って分解定理を表しているので注意を要する.この意味では,
を使って分解定理を表しているので注意を要する.この意味では, は無限個の
は無限個の
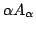 の「結び」として得られるというより「重ね合わせ」によって得られると理解した方がよいと思われる.
分解定理のいわんとするところを理解するためには,
の「結び」として得られるというより「重ね合わせ」によって得られると理解した方がよいと思われる.
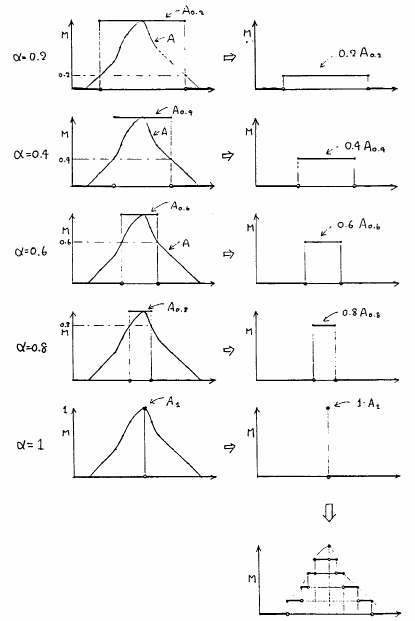
分解定理のいわんとするところを理解するためには, を離散的にとって考えてみるとわかりやすい.図4.22に
を離散的にとって考えてみるとわかりやすい.図4.22に が
が
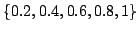 の有限の離散値しかとらないとした場合を示している.有限個の
の有限の離散値しかとらないとした場合を示している.有限個の レベル集合の
レベル集合の 倍の重ね合わせとして,階段状のファジィ集合が合成され,これが元のファジィ集合
倍の重ね合わせとして,階段状のファジィ集合が合成され,これが元のファジィ集合 を近似することがわかる.ここで
を近似することがわかる.ここで の値が区間
の値が区間![$(0,1]$](img232.gif) の任意の値を連続的にとるとすれば,合成されたファジィ集合は,元のファジィ集合
の任意の値を連続的にとるとすれば,合成されたファジィ集合は,元のファジィ集合 と完全に一致するであろうことは容易に推測される.
と完全に一致するであろうことは容易に推測される.
図 4.22
分解定理
 |
上にみたように, レベル集合を用いると,ファジィ集合をクリスプ集合の集まりとして表現できる.ファジィ集合を
レベル集合を用いると,ファジィ集合をクリスプ集合の集まりとして表現できる.ファジィ集合を レベル集合の集まりとしてとらえると,メンバシップ関数として直接とらえる場合より,ファジィ集合間の写像を求める場合にその取扱いが簡単になる.つまり,あるファジィ集合の像を求めるには,そのファジィ集合の
レベル集合の集まりとしてとらえると,メンバシップ関数として直接とらえる場合より,ファジィ集合間の写像を求める場合にその取扱いが簡単になる.つまり,あるファジィ集合の像を求めるには,そのファジィ集合の レベル集合の個々の像を求め,その写像結果を再構成すれば,所望のファジィ集合,即ち元のファジィ集合の像が得られるのだ.ここで実際に写像される個々の
レベル集合の個々の像を求め,その写像結果を再構成すれば,所望のファジィ集合,即ち元のファジィ集合の像が得られるのだ.ここで実際に写像される個々の レベル集合はクリスプ集合であるため取扱いが容易となる.
連続な形状を持つメンバシップ関数を表現するには,無限個の
レベル集合はクリスプ集合であるため取扱いが容易となる.
連続な形状を持つメンバシップ関数を表現するには,無限個の レベル集合が必要となるが,実際のシステムでは,無限個の
レベル集合が必要となるが,実際のシステムでは,無限個の レベル集合を用いることはできない.しかし,ディジタル・システムでは,もともとグレードが連続値ではなく量子化されていることを考えれば,最大でも量子化レベル数の
レベル集合を用いることはできない.しかし,ディジタル・システムでは,もともとグレードが連続値ではなく量子化されていることを考えれば,最大でも量子化レベル数の レベル集合をデータとして持てば十分であることがわかる.
ファジィ集合の写像に限らず,ファジィ集合間の演算:交わりと結びについても,
レベル集合をデータとして持てば十分であることがわかる.
ファジィ集合の写像に限らず,ファジィ集合間の演算:交わりと結びについても,
と レベル集合同士の演算として取り扱えると文献に紹介されている例があるが,これは,
レベル集合同士の演算として取り扱えると文献に紹介されている例があるが,これは,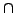 と
と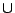 がそれぞれ論理積(
がそれぞれ論理積(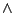 )と論理和(
)と論理和(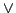 )によって定義されているときのみで,しかも,否定の演算には成立しないことに注意する必要がある.
)によって定義されているときのみで,しかも,否定の演算には成立しないことに注意する必要がある.
平成12年5月17日
![\begin{displaymath}
A=\bigcup_{\alpha \in (0,1]}\alpha A_\alpha
\end{displaymath}](img235.gif)