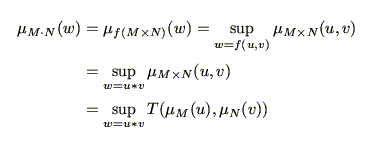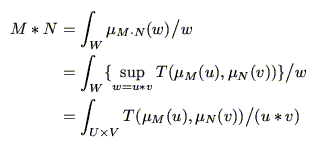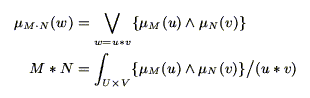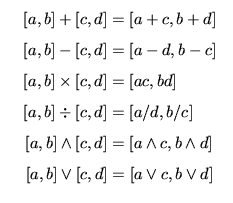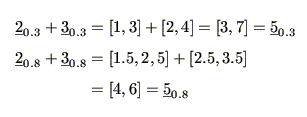


: 三角型ファジィ数とその計算
: ファジィ理論の数学的基礎
: 拡張原理
目次
ファジィ集合の中でも特に「だいたい10個」とか「約30才」などの概念は,実数直線上のファジィ集合として表され,特にファジィ数と呼ばれる.このファジィ数には数としての演算が定義でき,例えばファジィ数「だいたい5位」とファジィ数「だいたい3位」を足して,「だいたい8位」というファジィ集合を算出することが可能になる.
図 4.25
ファジィ数の例
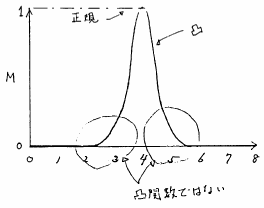 |
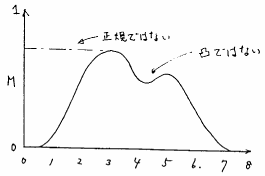
図 4.26
ファジィ数ではない実数直線上の連続ファジィ集合の例
|
|
ファジィ数とは,実数直線上で定義された正規かつ凸ファジィ集合で,特にメンバシップ関数が連続的なものをいう.
ここで,正規とは,メンバシップ関数の最大グレードが1であることを示す.また凸であるとは,メンバシップ関数に谷間の無いものをいう.例えば,図4.25はファジィ数「だいたい4位」の例である.これに対して,図4.26のファジィ集合は,実数直線上で連続なメンバシップ関数を持つが,正規でも凸でもないので,ファジィ数ではない.
ここで,凸なメンバシップ関数とは,通常の凸関数とは関係ないことに注意する.例えば,図4.25のファジィ数のメンバシップ関数は凸ではあるが,二次微分が正の部分があり凸関数ではない.
ファジィ数には,普通の実数のように演算を定義することができる.またもっと一般的には,ファジィ数には,関数を作用させることができる.即ち,ファジィ数はファジィ集合の一種であり,関数は写像の一種であることを考えると,4.7節の拡張原理がそのまま適用されるのがわかる.
例えば,いま二つのファジィ数
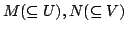 を考え,これらの間に,ある任意の数値間演算
を考え,これらの間に,ある任意の数値間演算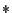 を作用させることを考える(例えば四則演算:
を作用させることを考える(例えば四則演算:
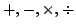 など).ここで,2数間の演算は,2変数の関数
など).ここで,2数間の演算は,2変数の関数
とみなすことができるから,演算結果(これもファジィ数である)
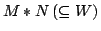 のメンバシップ関数は,4.7節の直積空間での拡張原理により,
のメンバシップ関数は,4.7節の直積空間での拡張原理により,
となる.したがって,ファジィ数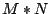 自体は,
自体は,
となる.ここで,4.2節のファジィ集合の表記法において,任意の要素に対して複数のグレードが得られた場合は,それらの間のグレードに対してsupをとってまとめられることに注意すれば,上式の最後の変形は理解される.
この定義は次のように読める.即ち,「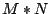 の
の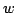 におけるグレードは,
におけるグレードは,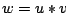 となるすべての組
となるすべての組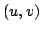 に対する
に対する
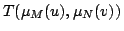 のうちで最大(厳密には上限)のものとする.」または「
のうちで最大(厳密には上限)のものとする.」または「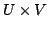 上のすべての要素
上のすべての要素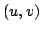 に対して演算
に対して演算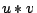 を行い,それらの結果の重ね合わせとして,
を行い,それらの結果の重ね合わせとして,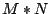 が得られる.」である.
ここで,通常の文献では,直積(もっと根本的には,結びを)定義する
が得られる.」である.
ここで,通常の文献では,直積(もっと根本的には,結びを)定義する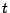 - ノルムとして,論理積(
- ノルムとして,論理積(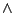 )を用いる場合だけを想定し,さらに上限をとる操作を最大をとる操作
)を用いる場合だけを想定し,さらに上限をとる操作を最大をとる操作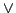 で代用して,ファジィ数の演算を
で代用して,ファジィ数の演算を
と定義している場合が多いが,これは,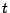 - ノルムに論理積を用いた特別な場合にだけ成立する定義であることに注意した方がよい.実際問題としては,計算の容易さなどから,ファジィ数を扱うときには,
- ノルムに論理積を用いた特別な場合にだけ成立する定義であることに注意した方がよい.実際問題としては,計算の容易さなどから,ファジィ数を扱うときには,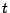 - ノルムに論理積を使う場合がほとんどのようである.
ファジィ数の演算は,先にみたように,拡張原理によって直接定義される.しかし,定義にしたがって計算すると,計算が複雑になり,また見通しが悪くなる場合が多い.つまり,上の定義にしたがって計算するには,
- ノルムに論理積を使う場合がほとんどのようである.
ファジィ数の演算は,先にみたように,拡張原理によって直接定義される.しかし,定義にしたがって計算すると,計算が複雑になり,また見通しが悪くなる場合が多い.つまり,上の定義にしたがって計算するには,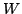 の任意の要素
の任意の要素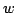 に対して演算結果が
に対して演算結果が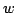 になるすべての組
になるすべての組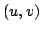 を見つけ出すか,最初からすべての
を見つけ出すか,最初からすべての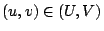 に対して演算を行う必要がある.そこで,4.7節で述べたNguyenの定理に基づき,
に対して演算を行う必要がある.そこで,4.7節で述べたNguyenの定理に基づき, レベル集合を介して演算する方法がよく用いられる.
レベル集合を介して演算する方法がよく用いられる.
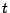 - ノルムとして論理積(
- ノルムとして論理積(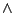 )を用いる場合は,ファジィ数間の直積の
)を用いる場合は,ファジィ数間の直積の レベル集合が,それぞれのファジィ数の
レベル集合が,それぞれのファジィ数の レベル集合の直積になるため演算は特に簡単になる.これは,区間分析法と呼ばれ次のように行われる.即ち,ファジィ数
レベル集合の直積になるため演算は特に簡単になる.これは,区間分析法と呼ばれ次のように行われる.即ち,ファジィ数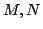 の
の レベル集合を与える区間集合(クリスプである)
レベル集合を与える区間集合(クリスプである)
を求めると,これらの区間集合の間の演算結果が,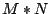 の
の レベル集合となる.即ち,
レベル集合となる.即ち,
である.したがって,すべての
![$\alpha\in (0,1]$](img297.gif) に対して,上式を求めて,最後に重ね合わせれば
に対して,上式を求めて,最後に重ね合わせれば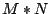 が求まる.但し,実際の計算には,
が求まる.但し,実際の計算には, の値として,
の値として,![$(0,1]$](img232.gif) の離散的な値について計算すれば十分であろう.ここでは,ファジィ数に対する演算は直接行っておらず,演算は,区間集合の場合についてのみ考えればよいことに注意する.区間集合間の代表的な演算に対する具体的な演算は,簡単な考察により,下のようになることがわかる.
の離散的な値について計算すれば十分であろう.ここでは,ファジィ数に対する演算は直接行っておらず,演算は,区間集合の場合についてのみ考えればよいことに注意する.区間集合間の代表的な演算に対する具体的な演算は,簡単な考察により,下のようになることがわかる.
区間間の演算結果は,それぞれの区間の要素のすべての組合せを考えて,演算結果が最小になるものと最大になるものが何かを考えれば容易に求まる.
図4.27 ファジィ数の計算の例(
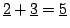 )
)
|
|
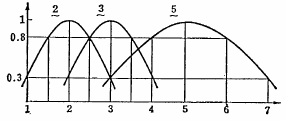
図4.27に「だいたい2位」を表すファジィ数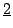 と「だいたい3位」を表すファジィ数
と「だいたい3位」を表すファジィ数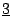 の和として「だいたい5位」が求まる例を示す.
の和として「だいたい5位」が求まる例を示す.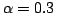 と
と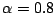 の
の レベル集合を見ると,
レベル集合を見ると,
が成立しているのがわかる.またファジィ数とファジィ数を演算すると結果のファジィ数の広がり(曖昧さ)が増加するのがわかる.
本節で説明した,ファジィ数間の演算は,ファジィ写像の特別な場合であり,あくまでもファジィ集合を数とみなした場合の数の間の演算としてとらえなくてはならない.ファジィ集合としての集合間の演算(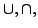 not()など)との区別に注意が必要である.感覚的には,ファジィ集合間の演算は,縦方向つまりメンバシップ関数の高さ方向の演算であるのに対して,ファジィ数間の演算は台集合方向の演算ととらえるとよい.
not()など)との区別に注意が必要である.感覚的には,ファジィ集合間の演算は,縦方向つまりメンバシップ関数の高さ方向の演算であるのに対して,ファジィ数間の演算は台集合方向の演算ととらえるとよい.
平成12年5月17日