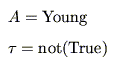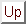


: ファジィ推論法の具体例の数学的解釈
: ファジィ推論の数学的解釈
: ルールが複数の場合の推論
目次
命題の真偽を表すために用いられる真理値として,最も基本的なものは,2値論理で用いられる真理値である.2値論理の真理値の定義域は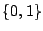 であり,これは,真(1)か偽(0)かのどちらかしか表せない.これでは,真偽の曖昧な命題を表せないため,この拡張として,提案されてきたのが,多値論理およびさらにその一般化としての無限値論理である.この無限値論理においては,真理値の定義域が区間
であり,これは,真(1)か偽(0)かのどちらかしか表せない.これでは,真偽の曖昧な命題を表せないため,この拡張として,提案されてきたのが,多値論理およびさらにその一般化としての無限値論理である.この無限値論理においては,真理値の定義域が区間![$[0,1]$](img106.gif) に拡張され,真理値は,この間の任意の実数値をとることができるようになった.
しかし,無限値論理では,例えば,ある命題が0.8真であるというような表現が可能となったが,なお,その真理値は0.8というように断定的なものであり,人間の言語生活上で用いる真偽の概念を表すには十分とはいえない.そこで,真理値を区間
に拡張され,真理値は,この間の任意の実数値をとることができるようになった.
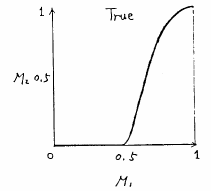
しかし,無限値論理では,例えば,ある命題が0.8真であるというような表現が可能となったが,なお,その真理値は0.8というように断定的なものであり,人間の言語生活上で用いる真偽の概念を表すには十分とはいえない.そこで,真理値を区間![$[0,1]$](img106.gif) 上のファジィ数に拡張したものが提案された.これが言語的真理値(Linguistic Truth Value, LTV)と呼ばれる(言語的真理値に対して,通常の無限値論理の真理値は,数値的真理値(Numerical Truth Value, NTV)と呼ばれる.).例えば人間の言葉で通常「真」と言っている概念は,図5.20のようなファジィ数Trueによって表すことが可能だろう(このメンバシップ関数の形はもちろん主観によって「真」の概念をうまく表すように適当に与えられる.).つまり真理値
上のファジィ数に拡張したものが提案された.これが言語的真理値(Linguistic Truth Value, LTV)と呼ばれる(言語的真理値に対して,通常の無限値論理の真理値は,数値的真理値(Numerical Truth Value, NTV)と呼ばれる.).例えば人間の言葉で通常「真」と言っている概念は,図5.20のようなファジィ数Trueによって表すことが可能だろう(このメンバシップ関数の形はもちろん主観によって「真」の概念をうまく表すように適当に与えられる.).つまり真理値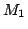 の値が1に近ければTrueである可能性
の値が1に近ければTrueである可能性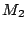 が高く,0.5以下だとTrueである可能性がない(
が高く,0.5以下だとTrueである可能性がない(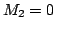 )ことを表している.
)ことを表している.
図 5.20
言語的真理値Trueの例
|
|
Trueに対する反意語としてFalseがあるが,これは,ファジィ数Trueに対して,否定演算子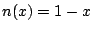 を作用させればよく,
を作用させればよく,
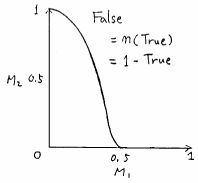
と得られる(4.8節参照).これを図示すると,Falseは図5.21のように得られる.これは図5.20のTrueを左右に反転した形になる.
図 5.21
言語的真理値Falseの例
|
|
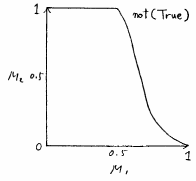
これに対して,Trueの否定not(True)はファジィ集合Trueの補集合であり,図5.22に示すように,図5.20のTrueを上下に反転した形となる.
図 5.22
言語的真理値not(True)の例
|
|
ある任意の言語的真理値を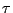 (
(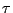 は当然
は当然![$[0,1]$](img106.gif) 上のファジィ数)としたとき,「
上のファジィ数)としたとき,「 is
is  」という命題に対して,
」という命題に対して,
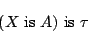 |
(5.14) |
と表現することを命題の言語的真理値限定と呼ぶ.これは,「 は
は であるという命題の真偽は
であるという命題の真偽は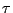 である」と読むことができそれ自身が新たな命題となっている.
例えば,
である」と読むことができそれ自身が新たな命題となっている.
例えば, を太郎の年齢を表す変数,
を太郎の年齢を表す変数,
とすれば,
となって,これは,「太郎が若いということは真ではない」ことを表す.ここで,「真」はファジィ数Trueの意味での「真」であることに注意する.
さて,式(5.14)は標準形になっていないが,これと同値の標準形の命題を求めることが可能である.即ち,
を満たすような,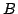 を求めることが可能である.結果から述べると,
を求めることが可能である.結果から述べると,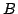 のメンバシップ関数は,
のメンバシップ関数は,
と求められる.これは,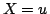 である可能性が,
である可能性が,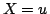 のときの「
のときの「 is
is  」の数値的真理値
」の数値的真理値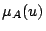 がTrueである可能性に等しいことを示している.
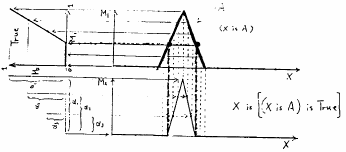
上の操作を図上で実現すると図5.23のようになる.図の上段の
がTrueである可能性に等しいことを示している.
上の操作を図上で実現すると図5.23のようになる.図の上段の
なる命題に対して
なる言語的真理値によって真理値限定を行ったとき,これと等価な標準形命題を
([( is
is  ) is True]は等価な標準形命題を与えるファジィ集合)とすれば,図のように,
) is True]は等価な標準形命題を与えるファジィ集合)とすれば,図のように, の各グレードを関数
の各グレードを関数
によって変換することによってファジィ集合[( is
is  ) is True]のメンバシップ関数の各グレードが得られる(注意:この説明図では,図の簡単化のため,言語的真理値Trueを折れ線型のメンバシップ関数で定義している.また言語的真理値を横倒しにして表示しているので注意.).
) is True]のメンバシップ関数の各グレードが得られる(注意:この説明図では,図の簡単化のため,言語的真理値Trueを折れ線型のメンバシップ関数で定義している.また言語的真理値を横倒しにして表示しているので注意.).
図 5.23
言語的真理値限定命題の標準形の誘導
|
|
図 5.24
種々の言語的真理値限定に対する標準形(1)
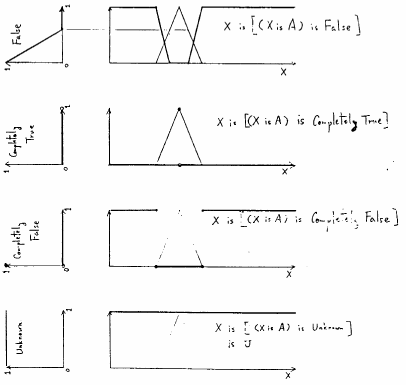 |
図 5.25
種々の言語的真理値限定に対する標準形(2)
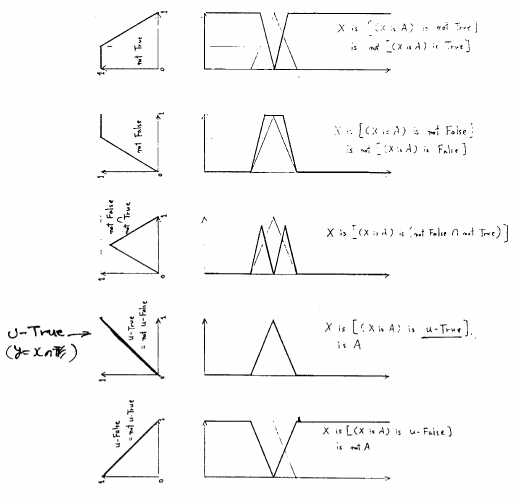 |
図 5.26
言語的真理値限定命題の具体例(その1)
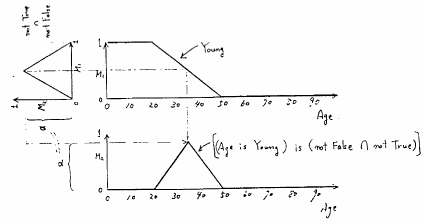 |
図 5.27
言語的真理値限定命題の具体例(その2)
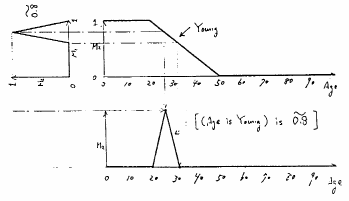 |
図5.24,図5.25に種々の言語的真理値によって「 is
is  」を限定した結果得られる標準形命題を図示するが非常に興味深い結果が推論されるのがわかる.
もっと具体的な例として,図5.26に
」を限定した結果得られる標準形命題を図示するが非常に興味深い結果が推論されるのがわかる.
もっと具体的な例として,図5.26に
なる命題から,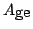 の可能性分布として,図5.26の下段のような結果が得られている.これは,「年が若いということが真とも偽ともいえない」という命題から,「年がだいたい35才位である」という結果を推論されることを示すものである.ここで,概念としては「Young」と「True」の定義を(メンバシップ関数として)与えただけであるのに,推論結果として,「35才位」という結果が推論されることに注目すべきであろう.
の可能性分布として,図5.26の下段のような結果が得られている.これは,「年が若いということが真とも偽ともいえない」という命題から,「年がだいたい35才位である」という結果を推論されることを示すものである.ここで,概念としては「Young」と「True」の定義を(メンバシップ関数として)与えただけであるのに,推論結果として,「35才位」という結果が推論されることに注目すべきであろう.
図 5.28
言語的真理値限定のタイプ2ファジィ集合上での解釈
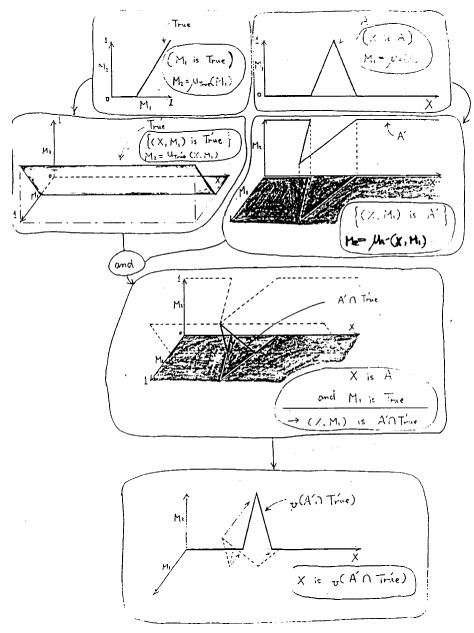 |
図5.27は「だいたい8割がた真」という言語的真理値で限定した例を示しているが,これに対しても「25才位」という推論結果が得られており,人間の常識な推論とうまく整合しているように思われる.
前項では,言語的真理値を特徴付けるメンバシップ関数をグレードを変換する関数とみなし,言語的真理値限定された命題の標準形を求めた.ここでは,タイプ2ファジィ集合を用いれば,ファジィ推論によって言語的真理値限定された命題の標準形が得られることを示そう.
例として,図5.23の言語的真理値によって限定された命題
(

is

) is True
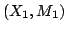 を変数とする命題に置き換えることを考える.
まず,
を変数とする命題に置き換えることを考える.
まず, は,これをタイプ2ファジィ集合とみなせば,図5.28に示すようなメンバシップ関数
は,これをタイプ2ファジィ集合とみなせば,図5.28に示すようなメンバシップ関数
を持つタイプ2ファジィ集合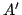 になるから,
と置き換えられる.
次に,TrueのCylindrical Extention
になるから,
と置き換えられる.
次に,TrueのCylindrical Extention
True
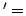
True
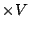
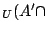 True
True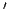 )は図5.23でグレードの変換で得られたファジィ集合に一致することは,図5.28を見れば明らかであろう.
言語的真理値のうちで,図5.29に示すようなメンバシップ関数,つまり
)は図5.23でグレードの変換で得られたファジィ集合に一致することは,図5.28を見れば明らかであろう.
言語的真理値のうちで,図5.29に示すようなメンバシップ関数,つまり
を持つ,一種の「真」を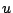 -True (Unitary True)と呼ぶ.この
-True (Unitary True)と呼ぶ.この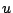 -Trueは図5.25の下から2段目に示すように,
なる関係を満たす言語的真理値である.言い替えると命題の標準形は実は,
-Trueは図5.25の下から2段目に示すように,
なる関係を満たす言語的真理値である.言い替えると命題の標準形は実は,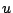 -Trueによって言語的真理値限定された命題とみなすことも可能である.この
-Trueによって言語的真理値限定された命題とみなすことも可能である.この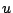 -Trueは,数値的真理値そのものが「真」であることの可能性と一致するような「真」の概念を与えているといえる.
-Trueは,数値的真理値そのものが「真」であることの可能性と一致するような「真」の概念を与えているといえる.
図 5.29
言語的真理値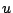 -Trueとその反意および否定
-Trueとその反意および否定
 |
この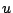 -Trueの否定not(
-Trueの否定not(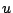 -True)と反意
-True)と反意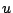 -Falseを求めると図5.28に見るようにまったく一致することがわかる.したがって,図5.25の最下段に見られるように,
も,
共に,
-Falseを求めると図5.28に見るようにまったく一致することがわかる.したがって,図5.25の最下段に見られるように,
も,
共に,

is not(

)
と, の補集合による標準形を導くという特徴がある.つまり
の補集合による標準形を導くという特徴がある.つまり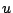 -Trueにより特徴付けられる「真」の概念は,「真ではない」と「偽である」ことを同一視するような真偽の概念を誘導するとみることができる.
このように見ると,命題の表現に言語的真理値による限定を導入する以前,即ち,標準形だけで命題を表現していた場合には,
-Trueにより特徴付けられる「真」の概念は,「真ではない」と「偽である」ことを同一視するような真偽の概念を誘導するとみることができる.
このように見ると,命題の表現に言語的真理値による限定を導入する以前,即ち,標準形だけで命題を表現していた場合には,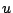 -Trueの誘導する真偽の概念しか用いていなかったことになり,この場合は,「偽である」ことと「真でない」ことの区別ができなかったことがわかる.しかし,人間の言語生活を鑑みると「偽である」こと「真でない」ことを違う概念として扱っていると思われ,この意味で,言語的真理値限定を用いた推論が,より人間の推論に近づきうる可能性を示唆しているものと受け取ることができよう.
-Trueの誘導する真偽の概念しか用いていなかったことになり,この場合は,「偽である」ことと「真でない」ことの区別ができなかったことがわかる.しかし,人間の言語生活を鑑みると「偽である」こと「真でない」ことを違う概念として扱っていると思われ,この意味で,言語的真理値限定を用いた推論が,より人間の推論に近づきうる可能性を示唆しているものと受け取ることができよう.



: ファジィ推論法の具体例の数学的解釈
: ファジィ推論の数学的解釈
: ルールが複数の場合の推論
目次
平成12年5月17日