


: ファジィ理論の図形,画像分野における応用例
: ファジィ推論の数学的解釈
: 言語的真理値に基づく推論
目次
3.2のファジィ推論法1の数学的解釈については,既に5.3節,5.4節で述べた.これは,タイプ1ファジィ集合のみによる最もオーソドックスなファジィ推論の方法であり,特に,本報告で紹介した推論法1は,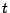 - ノルムを論理積で定義し,含意としてMandaniの含意を採用した場合にあたる.また3.1節で推論法1のバリエーションとして紹介した方法は,
- ノルムを論理積で定義し,含意としてMandaniの含意を採用した場合にあたる.また3.1節で推論法1のバリエーションとして紹介した方法は,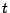 - ノルムを代数積で定義して,Mandaniの含意を採用した場合と解釈できる.一般に,推論法1は
- ノルムを代数積で定義して,Mandaniの含意を採用した場合と解釈できる.一般に,推論法1は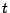 - ノルムの選び方とファジィ含意の定義の仕方の組合せによって多くのバリエーションが考えられる.
推論法2は推論法1において各ルールで求められる適合度によって後件部のファジィ命題を真理値限定しているものと考えられる.ここで,適合度は,区間
- ノルムの選び方とファジィ含意の定義の仕方の組合せによって多くのバリエーションが考えられる.
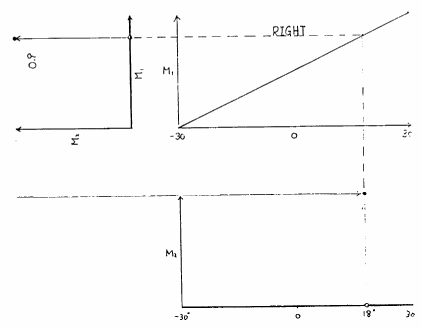
推論法2は推論法1において各ルールで求められる適合度によって後件部のファジィ命題を真理値限定しているものと考えられる.ここで,適合度は,区間![$[0,1]$](img106.gif) の間のある一つの実数の形で得られるため,適合度で真理値限定された後件部の標準形は,元の後件部のグレードが適合度と一致するところで,グレード1をとり,その他でグレード0となるクリスプ集合によって得られる.例えば適合度が0.8とした場合,これによる「
の間のある一つの実数の形で得られるため,適合度で真理値限定された後件部の標準形は,元の後件部のグレードが適合度と一致するところで,グレード1をとり,その他でグレード0となるクリスプ集合によって得られる.例えば適合度が0.8とした場合,これによる「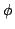 is RIGHT」の真理値限定
is RIGHT」の真理値限定
(
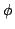
is RIGHT) is 0.8
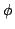
is 18
なる標準形を得る.これは,丁度,ファジィ集合RIGHTのメンバシップ関数上でグレードが0.8になるところを求めて,そこから垂直におりて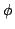 の値を読むことと同じ結果を与えている.
の値を読むことと同じ結果を与えている.
図 5.30
適合度による真理値限定
 |
推論法2はこのようにして,各ルールの結論を得て,さらに,それぞれの適合度によって重み付けした結果を最終的な結果として得ている.
推論法2をファジィ理論に基づいてもっと統一的にしかも厳密に解釈するには,タイプ2ファジィ集合上での含意命題の与え方に関してもっと立ち入った議論をする必要がある.これについては別の機会に報告することとする.
推論法3は,推論法1の の値の全体集合
の値の全体集合 として,
として, を変数とする線形式の全体を選んだもの,つまり,
を変数とする線形式の全体を選んだもの,つまり,
と解釈すれば,推論法1の特別な場合と解釈できる.例えば,図3.10の第1番目のルールの後件部は,
に対してグレード1を与えて,その他の任意の線形式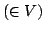 に対してはグレード0を与えていると解釈すればよい.
最終的に適合度によって重みつき平均をとっているが,これは,推論法1において,最後にそれぞれの結果の重ね合わせの重心をとっていることに対応する.
このように考えると,
に対してはグレード0を与えていると解釈すればよい.
最終的に適合度によって重みつき平均をとっているが,これは,推論法1において,最後にそれぞれの結果の重ね合わせの重心をとっていることに対応する.
このように考えると,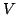 として何も線形式の全体を選ばなくてはならない必然性はなく,一般に,適当なモデルの全体集合を
として何も線形式の全体を選ばなくてはならない必然性はなく,一般に,適当なモデルの全体集合を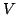 として与えることも可能であると思われる.例えば,適当なモデル
として与えることも可能であると思われる.例えば,適当なモデル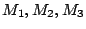 を考え,
を考え,
なる有限全体集合を考えてもよい.そして,例えば,3つのルールがそれぞれ,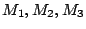 を結論とする場合は,
とすれば(後件部において4.1節で述べた有限ファジィ集合のベクトル表現を用いていることに注意),全体の推論結果として,それぞれのルールの適合度
を結論とする場合は,
とすれば(後件部において4.1節で述べた有限ファジィ集合のベクトル表現を用いていることに注意),全体の推論結果として,それぞれのルールの適合度
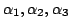 に応じて,全体の推論結果
に応じて,全体の推論結果
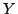
is
![$[\alpha_1,\alpha_2,\alpha_3]$](img509.gif)
が得られる.これに対して,例えば重心を求めれば,ある一つのモデル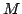 が
が
が推論される.
平成12年5月17日