クリスプ集合に対する可能性測度と必然性測度

本節では，まず可能性，必然性とはどのようなものかを感覚的につかむために，クリスプな集合のばあいだけを考えて考察する． さて，ある全体集合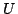$U$の中の二つの部分集合（クリスプ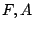）$F,A$を考える．そしていま，

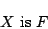$$\mbox{$X$\ is $F$}$$ (5.1)

だとわかっているとする．つまりこれは「$X$は$F$の要素である」とわかっていることを意味する．このとき，

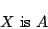$$\mbox{$X$\ is $A$}$$ (5.2)

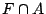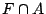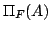ということ，即ち「$X$は$A$の要素である」ということがありえるかどうかを考える．これが即ち「可能性」であるかないかを考えることである．すると，集合$F$と$A$の間に重複する部分があれば，つまり$F\cap A$が空集合でなければ，そういう可能性があって，重複する部分がなければ，つまり$F\cap A$が空集合であれば，そういう可能性がないことは容易にわかる．そこで，「$X$が$F$の要素であるとき，それが$A$の要素である可能性」を$\Pi_F(A)$と書き，そのような可能性があるとき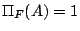，$\Pi_F(A)=1$，可能性が無いとき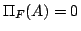，$\Pi_F(A)=0$と書くことにすれば，

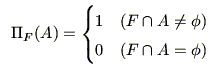
(5.3)

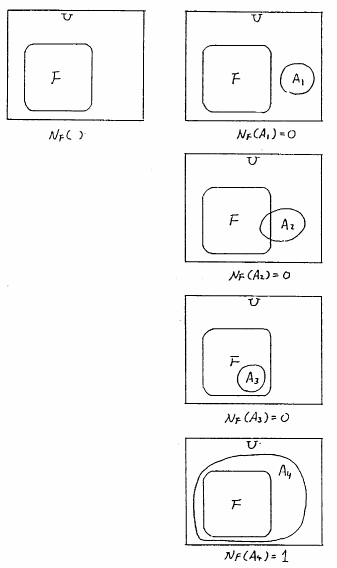
となる（図5.1参照）．

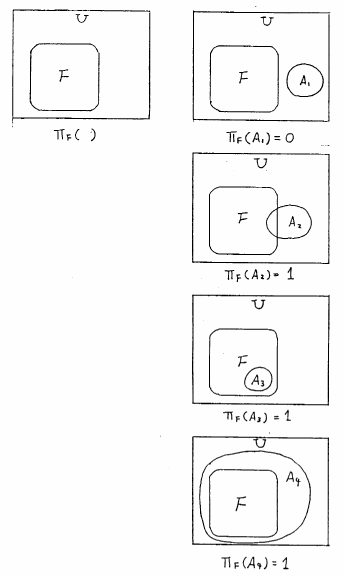
図 5.1   クリスプ集合の可能性測度の例

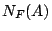一方，「$X$は$F$の要素である」（式(5.1)）とわかっているときに，「$X$は$A$の要素である」といえないはずはないといえるかどうかについて考える．これが即ち，そうである「必然性」があるかないかを考えることである．すると，これは，「$X$が$F$の要素であって$A$の要素でないことはない」といえるかどうかを考えていることであるから，集合$F$と集合$A$の補集合not($A$)の共通部分が無ければ，つまり $F\cap\mbox{not}(A)$が空集合であれば必然性があって，空集合でなければそういう必然性がないことは容易にわかる．そこで，「$X$が$F$の要素であるときに，それが$A$の要素である必然性」を$N_F(A)$と書き，そのような必然性があるとき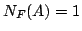，$N_F(A)=1$，必然性が無いとき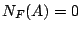，$N_F(A)=0$と書くことにすれば，

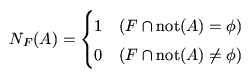
(5.4)

となる（図5.2参照）．

図 5.2   クリスプ集合の必然性測度の例

ここで，式(5.3)の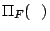$\Pi_F(~~)$と，式(5.4)の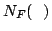$N_F(~~)$は関数とみたとき，全体集合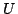$U$の部分集合の全体を定義域とし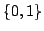，$\{0,1\}$を値域とする集合関数となっており，それぞれ次節で説明する可能性測度，必然性測度の特別な場合となっている．