


: 可能性限定命題と部分的無知
: ファジィ命題の可能性限定
: 可能性限定命題とその標準形
目次
前節では,可能性限定命題の標準形を天下り式に提示し,その意味をいささか強引に解釈した.ここでは,直観主義論理およびそれに様相性を取り入れた論理体系である様相論理の立場に立てば,可能性限定命題の標準形がもっと形式的にすっきり導出されることがわかったので,これについて説明する.ただしここで,ファジィ命題を他の論理体系で議論するための準備は第4章で述べるのでこれを参照されたい.
ここで用いるのは直観主義における「含意(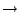 :ならば)の定義」と様相論理における「可能性の公理」および「必然性の公理」である.
:ならば)の定義」と様相論理における「可能性の公理」および「必然性の公理」である.
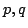 を命題とすると,直観主義論理における含意命題
を命題とすると,直観主義論理における含意命題
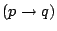 は,
は,
|
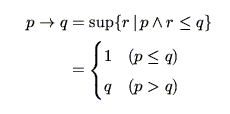
|
(2.9) |
と定義される.
また様相命題である「 は可能である」や「
は可能である」や「 は必然である」という命題はそれぞれ,可能性を表す論理記号
は必然である」という命題はそれぞれ,可能性を表す論理記号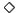 と必然性を表す論理記号
と必然性を表す論理記号 を用いて
を用いて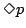 および
および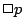 と表されるが,ここで,様相論理の立場では,最も基本的な公理として次の二つの公理を少なくとも認めている.即ち,
と表されるが,ここで,様相論理の立場では,最も基本的な公理として次の二つの公理を少なくとも認めている.即ち,
|
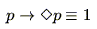
|
(2.10) |
|
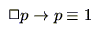
|
(2.11) |
である.ここで式(2.10)は「可能性の公理」と呼ばれ,「 であれば
であれば は可能である」ことが恒真であることを意味し,また式(2.11)は「必然性の公理」と呼ばれ,「
は可能である」ことが恒真であることを意味し,また式(2.11)は「必然性の公理」と呼ばれ,「 が必然であれば
が必然であれば である」ことを意味する.
ここで,式(2.9)の
である」ことを意味する.
ここで,式(2.9)の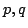 を
を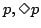 に置き換えれば,
に置き換えれば,
|
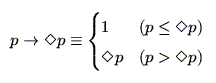
|
(2.12) |
が得られるが,これを式(2.10)の可能性の公理と比較すると,
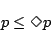 |
(2.13) |
となる.
また一方,式(2.9)の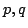 を
を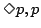 に置き換えれば,
に置き換えれば,
|
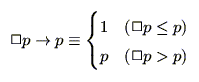
|
(2.14) |
が得られるが,これを式(2.11)の必然性の公理と比較すると,
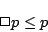 |
(2.15) |
となる.
さて,ここで,式(2.1)のなかの「 is
is  」を
」を
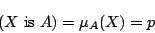 |
(2.16) |
とおけば,式(2.1)自身は(あるいはこれと同値な式(2.5)は),
 |
(2.17) |
となる.したがって,式(2.16)と式(2.17)を式(2.13)に代入すれば,
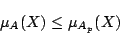 |
(2.18) |
なる条件が得られ,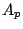 のメンバシップ関数が図2.2のようになることがわかる.
一方,式(2.3)は(あるいはこれと同値な式(2.7)は),
のメンバシップ関数が図2.2のようになることがわかる.
一方,式(2.3)は(あるいはこれと同値な式(2.7)は),
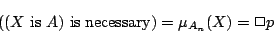 |
(2.19) |
となるが,ここで,式(2.19)と式(2.16)を式(2.15)に代入すれば,
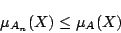 |
(2.20) |
なる条件が得られ,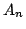 のメンバシップ関数が図2.4のようになることがわかる.
不可能性および偶然性については,それぞれ,可能性および必然性の否定概念であることは容易にわかるので,前節の議論で十分であろう.
のメンバシップ関数が図2.4のようになることがわかる.
不可能性および偶然性については,それぞれ,可能性および必然性の否定概念であることは容易にわかるので,前節の議論で十分であろう.



: 可能性限定命題と部分的無知
: ファジィ命題の可能性限定
: 可能性限定命題とその標準形
目次
平成12年5月17日