
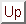


: FI論理の量子化定理
: ファジィ・インターバル論理
: ファジィ・インターバル(FI)論理の定義
目次
前節で,FI真理値が導入され,そのメンバシップが定義されたが,そのメンバシップ関数の定義自体については,議論の余地がありそうであった.しかし,ここで,メンバシップ関数の定義はさておき,FI真理値の代数的構造には非常に興味深いものがあるので,本節ではこれについて考察する.
いま,
![$X=[x_n,x_p],Y=[y_n,y_p]$](img402.gif) をFI真理値の任意の2要素とすると,FIにおける2種類の半順序関係が定義される.
をFI真理値の任意の2要素とすると,FIにおける2種類の半順序関係が定義される.
真偽の半順序関係
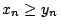 かつ
かつ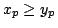 のとき,
のとき, と
と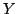 には真偽の半順序関係
には真偽の半順序関係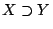 がある.
がある.
曖昧さの半順序関係
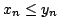 かつ
かつ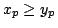 のとき,
のとき, と
と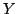 には曖昧さの半順序関係
には曖昧さの半順序関係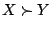 がある.
がある.
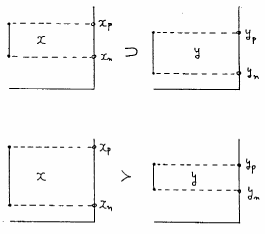
このように定義された2種類の半順序関係の典型的な例を図6.2に示す.
図 6.2
FI真理値の2種類の半順序関係の例
|
|
ここで,FI真理値の任意の2種類間には必ず,真偽の半順序関係か,曖昧さの半順序関係のどちらかの半順序関係が存在することは定義から容易にわかる.
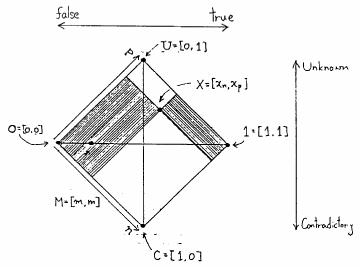
ところで,FI真理値は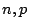 のペアによって決定されるから,図6.3のような正方形の1点と考えてよい.ここで,
のペアによって決定されるから,図6.3のような正方形の1点と考えてよい.ここで,![$0\equiv [0,0]$](img409.gif) (完全な偽),
(完全な偽),![$1\equiv [1,1]
$](img410.gif) (完全な真),
(完全な真),![$U\equiv [0,1]$](img411.gif) (完全な無知),
(完全な無知),![$C\equiv [1,0]$](img412.gif) (完全な矛盾)はそれぞれ,図6.3の4隅の点となる.またここで,あるFI真理値
(完全な矛盾)はそれぞれ,図6.3の4隅の点となる.またここで,あるFI真理値![$X=[x_n,x_p]$](img413.gif) と真偽の半順序関係にあるFI真理値の集合は図6.3の斜線を施した部分となり,曖昧さの半順序関係にあるFI真理値の集合は白く残した部分となる.さらに,通常の区間真理値の集合は,0と1を結んだ線より上の部分となり,無限値論理の真理値(数値的論理値)の集合は0と1を結んだ線に対応している.
と真偽の半順序関係にあるFI真理値の集合は図6.3の斜線を施した部分となり,曖昧さの半順序関係にあるFI真理値の集合は白く残した部分となる.さらに,通常の区間真理値の集合は,0と1を結んだ線より上の部分となり,無限値論理の真理値(数値的論理値)の集合は0と1を結んだ線に対応している.
図 6.3
FI真理値の 平面上での表現
平面上での表現
|
|
ここで,FI真理値の2種類の半順序関係に基づいて,2組の否定,積演算,和演算が定義される.即ち,真偽値の半順序関係に基づいて,論理演算,
が定義され,また曖昧さの半順序関係に基づいて,曖昧演算,
が定義される(ここで,FI論理の論理否定,曖昧否定の記号として,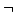 と
と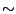 を用いているが,これは,第4章で定義した偽否定
を用いているが,これは,第4章で定義した偽否定 と直観主義否定
と直観主義否定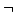 とは関係がないことに注意).
これを図示すれば,例えば,
とは関係がないことに注意).
これを図示すれば,例えば, と
と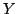 および
および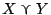 の関係は図6.4のようになる.これを同図上で解説すれば,
の関係は図6.4のようになる.これを同図上で解説すれば, の曖昧さの半順序関係に基づく上界と,
の曖昧さの半順序関係に基づく上界と,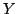 の曖昧さの半順序関係に基づく上界の共通部分,つまり
の曖昧さの半順序関係に基づく上界の共通部分,つまり と
と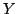 の共通上界の下限として得られているのがわかる.同様にして,他の例を図示すると,例えば,図6.5のような関係となっている.
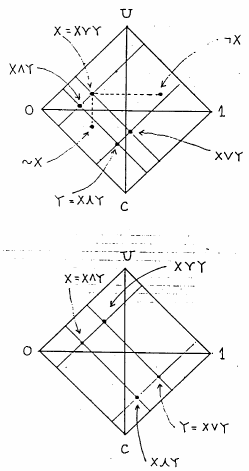
の共通上界の下限として得られているのがわかる.同様にして,他の例を図示すると,例えば,図6.5のような関係となっている.
図 6.4
曖昧積の例
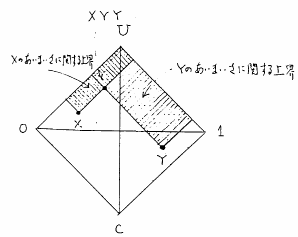 |
図 6.5
FI論理演算の例
 |
このFI真理値の集合は,このように二つの半順序関係が組み合わさった構造を持っているが,実は二つの半順序関係がそれぞれ,完備束の特別な場合であるド・モルガン代数となっていることは,それぞれが,無限値論理の真理値の集合と同型をしていることから容易に導かれる.このような代数的な構造を持つことから,FI論理では論理演算が容易に定義され,その代数的な構造が束にすらならない一般の言語的真理値に較べ,応用上の取扱いが格段に楽になる.またその一方では,FI真理値は「無知」や「矛盾」の概念を表すことができる,表現力の豊かな真理値モデルとなっている.このことから,FI論理は応用上非常に強力な道具となると期待されている.
平成12年5月17日