


: 可能性,必然性と区間真理値
: ファジィ論理と種々の論理体系
: 様相論理
目次
本節では,ファジィ理論と前節までに紹介した種々の論理体系とのかかわりについて述べる.
数学的な議論は通常,古典論理の上で行っており,いままでの本報告書のファジィ理論に関する議論自体もそうであった.これは,真,偽をはっきりさせる議論を行っているためである.また,ファジィ理論に基づくアルゴリズムも,それを実際に計算機上で実現するためには,最終的なプログラムの段階で古典論理に置き換えられていなくてはならない.なぜなら,計算機自体がcBa上の論理回路だけで構成されているからである.このように,ファジィ理論(あるいはファジィ論理)といっても結局は古典論理上で議論なりアルゴリズムの構築なりを行っていることになる.また,だからこそ,ファジィ理論が理論足り得るわけだし,ファジィ応用システムが現実に稼動しているのである.ファジィ理論自体が曖昧ではお話にならない.ファジィ理論は,古典論理的には,直接的にはっきり表せないような問題を(日常会話で,「論理的でない」といわれるような問題)をいかに論理的に表現するかという手段を与える古典論理上の理論である.つまり,ファジィ理論は,ファジィ論理(曖昧さを含む論理)を扱うために,古典論理の上に定義された理論である.これは,古典論理を包含している直観主義論理や様相論理が,その包含しているはずの古典論理上で議論されるのと同じ事情である.
当たり前のことだが,ここで確認しておくと,
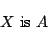 |
(4.42) |
なるファジィ命題は,古典論理上で,
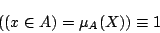 |
(4.43) |
であることだと定義されたのである.つまり「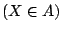 と表される
と表される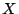 の関数が,
の関数が,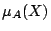 なる関数と同じであることが恒真である」と古典論理上で定義されたのである.ここで,古典論理は
なる関数と同じであることが恒真である」と古典論理上で定義されたのである.ここで,古典論理は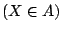 や
や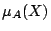 の値が何物なのか,何を意味するのかということに関しては,なんら関知していない.ただ,それらが恒等であることを定義として受け入れているにすぎない.それらがファジィ集合
の値が何物なのか,何を意味するのかということに関しては,なんら関知していない.ただ,それらが恒等であることを定義として受け入れているにすぎない.それらがファジィ集合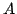 に
に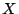 が含まれているということのグレードや真理値を与えているというような意味付けは,他の論理なり哲学なりが行うことで古典論理の知ったことではないのである.また,ファジィ命題,
が含まれているということのグレードや真理値を与えているというような意味付けは,他の論理なり哲学なりが行うことで古典論理の知ったことではないのである.また,ファジィ命題,
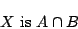 |
(4.44) |
は,古典論理上で,
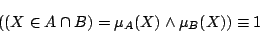 |
(4.45) |
と定義されるが,これにしても,古典論理は中の等号関係が恒に成立していることを定義として受け入れているだけで,これが共通集合の定義を与えていることなどはもちろんのこと,等号の両側にある値が真理値としての意味を持つことさえ,いっさい関知していない.この定義の意味付け自体は,他の論理,他の哲学が与えている.
ファジィ理論自体は,このように,曖昧な論理というものを哲学的に考察して,曖昧な論理における公理を探し,それを古典論理上に定義としてゆくことによって作られる体系であるといえる.古典論理上で定義されれば,あとは(古典論理の公理系の範囲内で)議論を真,偽をはっきりさせながら進めることができる.
実は,ファジィ論理に限らず,他の論理体系について古典論理上で議論することは通常行われていることである.またさらに,様々な論理体系を,統一的に,また形式的に取り扱うためのひな型ともいえる形式論理がGentzenによって生み出され,その上でそれぞれの論理体系を表して,相互の論理体系間の関係を調べる研究も多く行われている.したがって論理体系に関する議論は,この形式論理に沿ってすすめればさらに厳密に取り扱えるのだが,筆者はいまだ形式論理に明るくないので,ここでは,これ以上ふれないことにする.
タイプ1のファジィ集合では,メンバシップ関数のグレードが,閉区間![$[0,1]$](img15.gif) の中にある実数として定義されている.ここで,あるメンバのグレードは,「そのメンバがメンバシップ関数により定義されるファジィ集合に含まれている」という命題に対する真理値を与えていると考えてきた.つまり,メンバシップ関数のグレードは真理値そのものであり,これが区間
の中にある実数として定義されている.ここで,あるメンバのグレードは,「そのメンバがメンバシップ関数により定義されるファジィ集合に含まれている」という命題に対する真理値を与えていると考えてきた.つまり,メンバシップ関数のグレードは真理値そのものであり,これが区間![$[0,1]$](img15.gif) で定義されるということは,真理値の集合として,区間
で定義されるということは,真理値の集合として,区間![$[0,1]$](img15.gif) を仮定していることに他ならない.ここで,4.2節,4.3節でみてきたように,区間
を仮定していることに他ならない.ここで,4.2節,4.3節でみてきたように,区間![$[0,1]$](img15.gif) は束として見た場合,cHaにはなっているが,cBaにはなっていない.したがって,これから,真理値の集合として区間
は束として見た場合,cHaにはなっているが,cBaにはなっていない.したがって,これから,真理値の集合として区間![$[0,1]$](img15.gif) を仮定するタイプ1ファジィ集合は,古典論理ではなく直観主義論理上の概念であることがわかる.
さてここで,真理値集合を閉区間
を仮定するタイプ1ファジィ集合は,古典論理ではなく直観主義論理上の概念であることがわかる.
さてここで,真理値集合を閉区間![$[0,1]$](img15.gif) としたときに,それぞれの論理演算が具体的にどのように定義されるかをみてみよう.
まず古典論理的な否定(
としたときに,それぞれの論理演算が具体的にどのように定義されるかをみてみよう.
まず古典論理的な否定(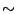 ,擬否定)として,
,擬否定)として,
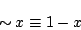 |
(4.46) |
を定義することができる.これは![$[0,1]$](img15.gif) で擬否定としての性質,式(4.11)と式(4.12)を満足する論理演算となっている(前報告書
で擬否定としての性質,式(4.11)と式(4.12)を満足する論理演算となっている(前報告書![${}^{[1]}$](img13.gif) で報告したように,このような性質を満たす否定演算は他にも考えられる.).
次に,含意演算は式(4.14)により,
で報告したように,このような性質を満たす否定演算は他にも考えられる.).
次に,含意演算は式(4.14)により,
|
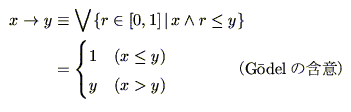
|
(4.47) |
となる.これは,Godelの含意と呼ばれるものである.
もちろんここで,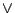 と
と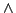 は通常の実数の大小関係に基づくmin,maxの演算である.
このように,直観主義論理に従えばタイプ1のファジィ集合における含意演算は,式(4.47)のGodelの含意となるのが当然のように思える.しかし,
は通常の実数の大小関係に基づくmin,maxの演算である.
このように,直観主義論理に従えばタイプ1のファジィ集合における含意演算は,式(4.47)のGodelの含意となるのが当然のように思える.しかし,![$[0,1]$](img15.gif) 上の含意としては種々のものが現在までに定義されており,前報告書で報告したように,ファジィ理論の含意としても種々のものが用いられているのが現状である.例えばZadehの含意は,
上の含意としては種々のものが現在までに定義されており,前報告書で報告したように,ファジィ理論の含意としても種々のものが用いられているのが現状である.例えばZadehの含意は,
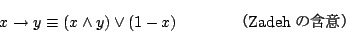 |
(4.48) |
と与えられるし,Lukasiewiczの含意は,
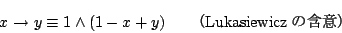 |
(4.49) |
と与えられる.またMandaniの含意は,
 |
(4.50) |
であった.他にも,
|
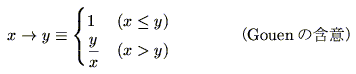
|
(4.51) |
|
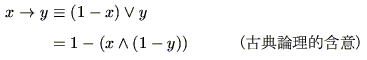
|
(4.52) |
など種々のものがある.
これらの数多くある含意演算は,どう解釈すればよいだろうか.Mandaniの含意(式(4.50))は含意を単に連言に置き換えたものとみるより他ないだろう.古典的含意(式(4.52))は,cHa上の「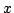 ならば
ならば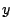 」に対して,cBa上の古典論理的な解釈「
」に対して,cBa上の古典論理的な解釈「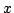 ではないかまたは
ではないかまたは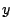 である」(式(4.52)の2行目の形では「
である」(式(4.52)の2行目の形では「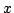 でありかつ
でありかつ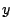 でないことはない」)を(この解釈は2値論理的に考えるからこそもっともらしいのにもかかわらず)強引に持ち込んだものと考えられる.Zadehの含意(式(4.48))は「
でないことはない」)を(この解釈は2値論理的に考えるからこそもっともらしいのにもかかわらず)強引に持ち込んだものと考えられる.Zadehの含意(式(4.48))は「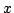 ならば
ならば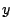 」を「
」を「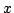 でかつ
でかつ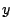 であるか,または
であるか,または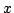 ではない」ことだと解釈していることに当たるが,この解釈も2値論理的に考えたcBa上での解釈であり,これをcHa上に強引に持ち込んでいるように考えられる.いずれにしても,これら三つの含意は,直観主義的な(つまり,式(4.15)のようなmodus ponensを満たすような含意を定義しようという立場にたった)含意とは関係なく,cBa上の古典論的な議論をそのままcHa上に強引に持ち込んだものと思われる.
それに対して,Lukasiewiczの含意(式(4.49))とGouenの含意(式(4.51))はある意味で,直観主義的な含意といえる.即ち,式(4.15)の中に現れる論理積
ではない」ことだと解釈していることに当たるが,この解釈も2値論理的に考えたcBa上での解釈であり,これをcHa上に強引に持ち込んでいるように考えられる.いずれにしても,これら三つの含意は,直観主義的な(つまり,式(4.15)のようなmodus ponensを満たすような含意を定義しようという立場にたった)含意とは関係なく,cBa上の古典論的な議論をそのままcHa上に強引に持ち込んだものと思われる.
それに対して,Lukasiewiczの含意(式(4.49))とGouenの含意(式(4.51))はある意味で,直観主義的な含意といえる.即ち,式(4.15)の中に現れる論理積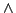 を限界積
を限界積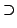 あるいは代数積
あるいは代数積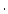 で置き換えたものが,
で置き換えたものが,
|
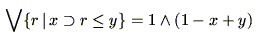
|
(4.53) |
|
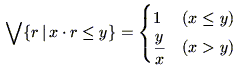
|
(4.54)
|
とそれぞれの含意に一致するのである.ただし,ここで,
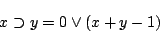 |
(4.55) |
である.これは,連言(かつ)の概念を表す演算として論理積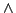 を用いないで,他の積演算(あるいは
を用いないで,他の積演算(あるいは ノルム)である,限界積,代数積を用いた場合,modus ponesを満たすような含意が,それぞれ,Lukasiewiczの含意,Gouenの含意であるということである.また,限界積とLukasiewicz含意,代数積のGouen含意の間にはそれぞれ随伴関係がある.
前報告書の段階では,
ノルム)である,限界積,代数積を用いた場合,modus ponesを満たすような含意が,それぞれ,Lukasiewiczの含意,Gouenの含意であるということである.また,限界積とLukasiewicz含意,代数積のGouen含意の間にはそれぞれ随伴関係がある.
前報告書の段階では,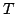 ノルムの選び方にかかわらず適当な含意を用いてよいとしたが,このように,modus ponensの成立に着目した場合,選んだ連言と随伴関係にある含意を選ぶことには意味のあることであろう.通常,ファジィ推論では,(
ノルムの選び方にかかわらず適当な含意を用いてよいとしたが,このように,modus ponensの成立に着目した場合,選んだ連言と随伴関係にある含意を選ぶことには意味のあることであろう.通常,ファジィ推論では,(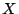 is
is 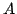 )と((
)と((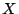 is
is 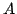 )
)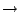 (
(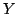 is
is 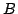 ))から,(
))から,(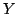 is
is 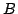 )が得られない,つまり,推論のレベルでのmodus ponensが成立しないことが指摘されているが,それは,その元となる論理演算の段階で,上のような随伴関係にある論理演算を使っていないからである.よくファジィ推論では,連言として論理積,含意としてZadehかLukasiewiczのものを用いるが,それらは,随伴関係にないのである.また,実際に,論理積とGodelの含意,代数積とGouen含意,限界積とLukasiewicz含意をそれぞれペアで用いれば,ファジィ推論のレベルにおいても,modus ponensが成立することが確かめられる.
上の含意の内で,Lukasiewiczの含意には,さらにおもしろい性質があることがわかる.限界積
)が得られない,つまり,推論のレベルでのmodus ponensが成立しないことが指摘されているが,それは,その元となる論理演算の段階で,上のような随伴関係にある論理演算を使っていないからである.よくファジィ推論では,連言として論理積,含意としてZadehかLukasiewiczのものを用いるが,それらは,随伴関係にないのである.また,実際に,論理積とGodelの含意,代数積とGouen含意,限界積とLukasiewicz含意をそれぞれペアで用いれば,ファジィ推論のレベルにおいても,modus ponensが成立することが確かめられる.
上の含意の内で,Lukasiewiczの含意には,さらにおもしろい性質があることがわかる.限界積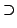 を論理積
を論理積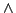 の代わりに用いれば,式(4.52)の古典論理的含意からも式(4.49)が導かれるのである.これは,Lukasiewicz含意が,限界積に対しても,直観主義論理的な意味からも,古典論理的な意味からも,含意となっていることを示している.
さらに,この連言と含意の随伴性はmodus ponensの成立に関する問題以外にファジィ・システムの逆問題や同定を解くために重要な役割を担っている.またここから可能性システムと必然性システムという双対ファジィ・システムが定義されることから,様相性にも大きなかかわりがある.しかし,現段階ではいまだこの点に関する詳細な検討を済ませていないのでここではこれ以上は述べないことにする.
タイプ2ファジィ集合のグレードつまり,言語的真理値は区間
の代わりに用いれば,式(4.52)の古典論理的含意からも式(4.49)が導かれるのである.これは,Lukasiewicz含意が,限界積に対しても,直観主義論理的な意味からも,古典論理的な意味からも,含意となっていることを示している.
さらに,この連言と含意の随伴性はmodus ponensの成立に関する問題以外にファジィ・システムの逆問題や同定を解くために重要な役割を担っている.またここから可能性システムと必然性システムという双対ファジィ・システムが定義されることから,様相性にも大きなかかわりがある.しかし,現段階ではいまだこの点に関する詳細な検討を済ませていないのでここではこれ以上は述べないことにする.
タイプ2ファジィ集合のグレードつまり,言語的真理値は区間![$[0,1]$](img15.gif) を台集合とするファジィ集合であった.この言語的真理値の自由度は大きく,人間が日常の生活で漠然と抱いている真理に関する概念をうまく表現するために有効であった.しかしその一方,言語的真理値の集合,即ち
を台集合とするファジィ集合であった.この言語的真理値の自由度は大きく,人間が日常の生活で漠然と抱いている真理に関する概念をうまく表現するために有効であった.しかしその一方,言語的真理値の集合,即ち![$[0,1]$](img15.gif) 上のファジィ集合のすべてを要素として集めた集合の代数的な構造は束にすらならないことが知られている.つまり,言語的真理値の集合は代数的な構造が非常に希薄であることを意味し,したがって,この上で代数的な論理演算を用いた論理体系を作ることはほとんど不可能であることを示している.言語的真理値は表現能力としては非常に大きいがその論理的な取扱いが非常に困難なのである.
そのため,言語的真理値のすべてを扱わないで,その特別な場合である,区間真理値や,ファジィ・インターバル論理における真理値だけを真理値の集合の要素として用いる方法が提案されている.これらの真理値を用いると,言語的真理値よりは表現の自由度がある程度制限されつつもなお言語的真理値の表現力の多くを継承しており,しかもその代数的な構造が強くなることにより論理演算がうまく定義されるようになる.
いずれにしても,タイプ2ファジィ集合の真理値は一般に幅を持つようになるのがタイプ1ファジィ集合と大きく異なる部分である.タイプ1ファジィ集合の真理値は常にある確定した幅を持つのに対して,タイプ2ファジィ集合の真理値は,一般にある値に確定しないで,幅を持つ.真理値に幅があるということは,その幅の中のどの真理値でもあり得る「可能性」があるということである.このような事情から,タイプ2ファジィ集合の真理値は様相性の概念と関係がありそうに思える.またこれは,第2章の可能性限定により,タイプ2ファジィ集合の真理値の特別の場合,即ち区間真理値が誘導されたことからみても明らかであろう.さらに,区間真理値やファジィ・インターバル論理の真理値では,可能性真理値,必然性真理値という概念が用いられている.
様相性と言語的真理値の関係については第5章で,また,ファジィ・インターバル論理と様相性に関しては第6章でさらに考察することにする.
上のファジィ集合のすべてを要素として集めた集合の代数的な構造は束にすらならないことが知られている.つまり,言語的真理値の集合は代数的な構造が非常に希薄であることを意味し,したがって,この上で代数的な論理演算を用いた論理体系を作ることはほとんど不可能であることを示している.言語的真理値は表現能力としては非常に大きいがその論理的な取扱いが非常に困難なのである.
そのため,言語的真理値のすべてを扱わないで,その特別な場合である,区間真理値や,ファジィ・インターバル論理における真理値だけを真理値の集合の要素として用いる方法が提案されている.これらの真理値を用いると,言語的真理値よりは表現の自由度がある程度制限されつつもなお言語的真理値の表現力の多くを継承しており,しかもその代数的な構造が強くなることにより論理演算がうまく定義されるようになる.
いずれにしても,タイプ2ファジィ集合の真理値は一般に幅を持つようになるのがタイプ1ファジィ集合と大きく異なる部分である.タイプ1ファジィ集合の真理値は常にある確定した幅を持つのに対して,タイプ2ファジィ集合の真理値は,一般にある値に確定しないで,幅を持つ.真理値に幅があるということは,その幅の中のどの真理値でもあり得る「可能性」があるということである.このような事情から,タイプ2ファジィ集合の真理値は様相性の概念と関係がありそうに思える.またこれは,第2章の可能性限定により,タイプ2ファジィ集合の真理値の特別の場合,即ち区間真理値が誘導されたことからみても明らかであろう.さらに,区間真理値やファジィ・インターバル論理の真理値では,可能性真理値,必然性真理値という概念が用いられている.
様相性と言語的真理値の関係については第5章で,また,ファジィ・インターバル論理と様相性に関しては第6章でさらに考察することにする.



: 可能性,必然性と区間真理値
: ファジィ論理と種々の論理体系
: 様相論理
目次
平成12年5月17日